Vous chantez le blues à faible volatilité ? Essayez les calendriers

L'un des avantages offerts par les stratégies d'options est le potentiel de profit à la hausse, vers le bas, ou des marchés limités à l'aire de répartition. Même sur des marchés calmes où la faible volatilité implicite maintient les prix des options stagnants, des opportunités potentielles peuvent être trouvées.

Au cours des dernières années, le marché boursier a connu des périodes de faible volatilité. En 2017 et 2018, par exemple, l'indice de volatilité Cboe (VIX ), l'indice de la peur du marché, ” a touché ses plus bas niveaux en 20 ans. Une stratégie d'options à considérer pendant les périodes de vol en sourdine est le spread calendaire («calendrier»).

Principes de base de la stratégie de calendrier

Un calendrier est la vente d'une option à court terme ainsi que l'achat d'une option à plus long terme du même type et d'exercice. C'est une stratégie à risque défini, avec le risque généralement limité au montant que vous avez payé pour le spread, ou le débit.

L'idée ici est que, tandis que le temps passe, l'option à court terme vendue se détériorera plus rapidement que l'option à plus long terme, et le commerce pourrait profiter si le spread peut être vendu plus cher que vous ne l'avez payé.

Avant d'aller plus loin, Revenons en arrière et regardons comment les prix des options réagissent aux changements de prix et à la volatilité implicite du sous-jacent, et avec le temps qui passe.

Comprendre les Grecs

Non, pas Zeus, Héra, et Apollon, mais plutôt delta, gamma, thêta, et vega. Ces grecs mesurent la sensibilité d'une option à divers facteurs qui peuvent affecter son prix. Pour apprécier pleinement la valeur des spreads calendaires, les traders doivent avoir au moins une compréhension de base du delta, thêta, et vega.

Delta est une mesure de la sensibilité d'une option aux variations du prix de l'action sous-jacente. Pour chaque mouvement de 1 $ dans le cours de l'action, le prix de l'option change du montant du delta. Par exemple, supposons qu'une action se négocie à 50 $, et l'appel à 50 grèves vaut 2 $ avec un delta de 0,5. Si le stock atteignait 51 $, Tout le reste est égal, l'appel aurait une nouvelle valeur théorique de 2,50 $.

Véga mesure la sensibilité d'une option aux variations de la volatilité sous-jacente, et est généralement coté en termes de variation de 1% de la volatilité. Par exemple, si une option a un vega de 0,04, une augmentation de 1 % de la volatilité augmenterait théoriquement la prime de l'option de 0,04 $, tout le reste était égal. En général, plus une option a de temps jusqu'à son expiration, plus son vega est haut.

Thêta, également connu sous le nom de "décroissance temporelle, " est une mesure de la sensibilité du prix d'une option au temps. Le prix d'une option, également connu sous le nom de « prime, ” se compose de la valeur intrinsèque (la différence positive entre le prix d'exercice de l'option et le prix de l'action sous-jacente) et la valeur extrinsèque (valeur temps). Theta estime de combien la valeur théorique de l'option diminue chaque jour. Le thêta d'une option à court terme décroît plus rapidement que celui des options à long terme. Ceci est essentiel à comprendre lorsque l'on discute des calendriers.

Ce qui suit, comme toutes nos discussions stratégiques, est strictement à des fins éducatives seulement. Ce n'est pas, et ne doit pas être considéré, un conseil individualisé ou une recommandation.

Exemple de stratégie :calendrier d'appels long

La figure 1 montre une chaîne d'options typique, et à titre d'exemple, nous avons mis en évidence les appels à 235 grèves de novembre (novembre) et décembre (décembre). Supposons qu'un trader d'options achète une option d'achat de décembre 235 au prix d'offre de 5,90 $ et vende une option d'achat de novembre 235 au prix d'achat de 3,70 $ (x le multiplicateur de contrat de 100), ou (5,90 $ - 3,70 $) x 100 =220 $ plus les frais de transaction. Notez les grecs dans le tableau ci-dessous :

0,37

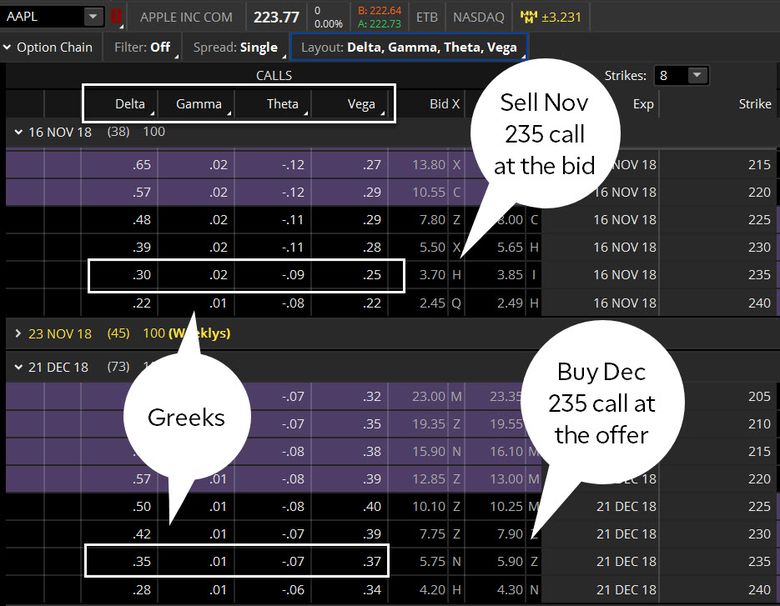FIGURE 1 :CHAÎNE D'OPTIONS. Acheter un calendrier d'appels sur le thinkorswim ^® plate-forme de TD Ameritrade. Notez les valeurs pour delta, gamma, thêta, et vega (les "grecs"). A titre indicatif seulement. Les performances passées ne garantissent pas les résultats futurs.

Voici comment les grecs peuvent nous aider à interpréter l'effet du temps et de la volatilité sur la valeur du spread d'option :

• Le delta du spread est de 0,05 (0,35 moins 0,30 =0,05). Puisque le delta est positif, cela signifie que le spread augmentera en valeur théorique à mesure que le cours de l'action sous-jacente augmentera, tout le reste était égal.
• Le thêta du spread est de 0,02 (-0,07 moins -0,09 =0,02), le spread gagnerait donc théoriquement 0,02 $ par jour.
• Le vega du spread est de 0,12 (0,37 moins 0,25 =0,12), la valeur de l'écart augmenterait donc de 0,12 $ si la volatilité n'augmentait que de 1 %.

Quel est notre objectif ici ?

Avec cet exemple de propagation, nous recherchons que le cours de l'action clôture près de la grève de 235 à l'expiration de novembre, mais de préférence en dessous, donc l'option Nov (la jambe courte) expirerait sans valeur. Le crédit que nous recevons pour l'appel de décembre aide à compenser une partie du coût de l'option de novembre (la longue étape). Et parce que la propagation a un vega positif, nous attendons également une éventuelle remontée de la volatilité. C'est pourquoi les calendriers peuvent être efficaces dans des environnements à faible volatilité.

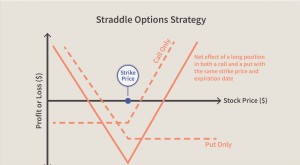
Notez que la même logique s'applique également aux spreads de calendrier. Tout le reste est égal, le potentiel de profit d'un calendrier culmine avec l'action sous-jacente au prix d'exercice à l'expiration de la jambe avant. Voir la figure 2. Rappelez-vous, bien que, qu'une option peut être exercée à tout moment avant l'expiration, donc si vous prévoyez de tenir un calendrier étalé jusqu'à l'expiration du premier mois, il est important de comprendre les tenants et aboutissants de l'expiration des options.

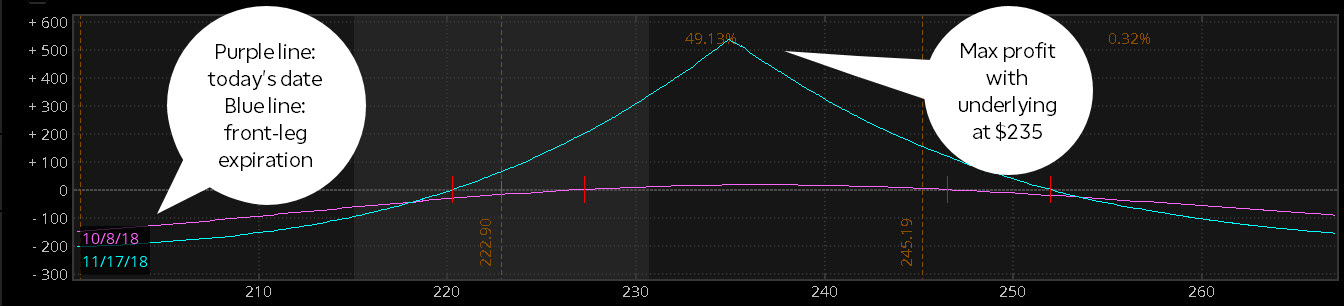
FIGURE 2 :CALENDRIER RÉPARTITION DES BÉNÉFICES À L'EXPIRATION DE LA JAMBE AVANT. Notez que le gain maximum du spread correspond au prix d'exercice à l'expiration du contrat de novembre. Source :La plateforme thinkorswim de TD Ameritrade. A titre indicatif seulement. Les performances passées ne garantissent pas les résultats futurs.

Les forces de la volatilité et du temps

L'un des avantages des calendriers est que vous n'avez pas besoin d'un mouvement de l'action sous-jacente pour voir la valeur théorique du spread augmenter. Rappelles toi, avec un long calendrier étalé, vous êtes thêta positif et long vega. Cela signifie que même si l'action sous-jacente reste inchangée, la valeur théorique du spread pourrait encore augmenter, soit par une augmentation de la volatilité (vega), ou le passage du temps (thêta).

Rappelles toi, le thêta du spread est de 0,02 (-0,09 moins -0,07 =-0,02), le spread gagne donc théoriquement 0,02 $ par jour (x le multiplicateur de contrat de 100, ou 2 $ par jour), tout le reste était égal. Un autre avantage d'avoir un thêta positif dans un écart calendaire est que la prime reçue pour l'option courte de novembre permet de compenser une partie du coût de l'option longue de décembre, jusqu'à ce que l'option de novembre perde sa valeur extrinsèque. Reportez-vous à la figure 2 pour voir la valeur du spread aujourd'hui (ligne violette) et à l'expiration de novembre (ligne bleue) représentée graphiquement par rapport au mouvement de l'action sous-jacente. Noter que, à l'approche de l'expiration de novembre, la ligne violette converge lentement vers la ligne bleue.

Sur la plateforme thinkorswim de TD Ameritrade, vous pouvez modéliser ce mouvement en faisant un clic droit sur un métier et en sélectionnant Analyser > Profil de risque . Entre le ticket de commande et le graphique, à côté de la date, vous verrez un " + ". La sélection qui fait passer l'analyseur de risques au jour suivant. Recommencez plusieurs fois et regardez les lignes converger.

Et n'oublions pas les effets de la volatilité. La figure 3 montre l'évolution de la valeur théorique du spread avec une hausse de 5 % de la volatilité. Le vega de la propagation est de 0,12. Augmentation de la volatilité de 5% dans l'analyseur de risque, et en gardant tout le reste égal, augmente la valeur théorique d'environ (0,12 $ x 5 x le multiplicateur de 100), ou environ 60 $.

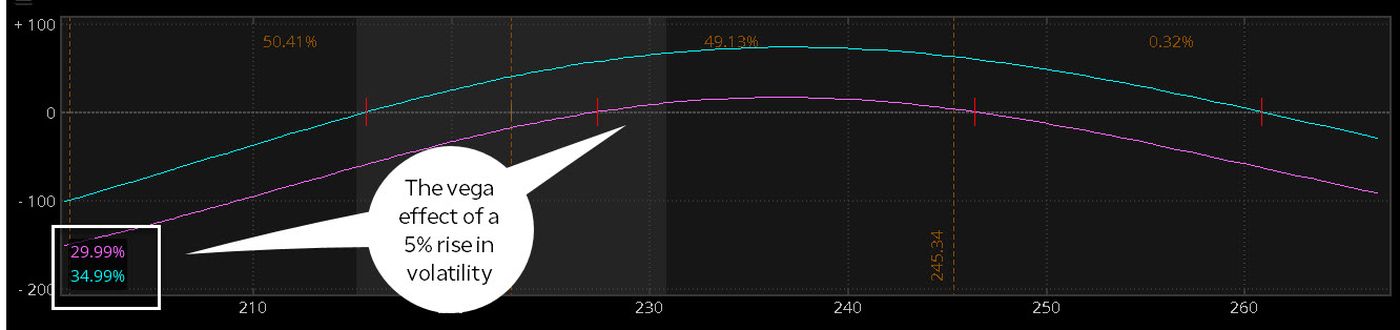FIGURE 3 :EFFET D'UNE HAUSSE DE LA VOLATILITÉ. Une hausse de 1% de la volatilité, tout le reste étant égal, augmenterait le prix théorique du spread d'environ 0,012 $, le vega de la propagation. On voit ici l'effet d'une hausse de 5%. La plateforme thinkorswim vous permet d'expérimenter différents scénarios tels que le temps et la volatilité. Vous pouvez même consulter le profil de risque si vous décidez de conserver l'option Dec après l'expiration de Nov. Source :La plateforme thinkorswim de TD Ameritrade. A titre indicatif seulement. Les performances passées ne garantissent pas les résultats futurs.

Les effets de la volatilité et du temps sur les spreads calendaires sont ce qui pourrait les rendre efficaces dans un environnement de marché calme ou à faible volatilité. Si le marché est au point mort, le thêta travaille théoriquement en votre faveur. Si le marché commence à bouger, et par conséquent la volatilité augmente, vous pourriez bénéficier du vega positif de la propagation. Mais, comme pour toutes les transactions sur options, il y a des risques. Si l'action sous-jacente s'éloignait suffisamment de la grève, vous commenceriez à perdre la valeur extrinsèque de la longue jambe. Et ce n'est pas parce que la volatilité est faible qu'elle ne peut pas baisser. Vega fonctionne dans les deux sens.

Les marchés sont dynamiques :il y a des périodes actives et des périodes creuses, volatilité élevée et volatilité faible. Si vous êtes un trader d'options qui chante occasionnellement le blues à faible volume, pensez à jeter un œil aux calendriers pour vous aider à trouver la bonne note.

Les options sont-elles bon choix pour vous?

Alors que le trading d'options implique des risques uniques et ne convient certainement pas à tout le monde, si vous pensez que le trading d'options correspond à votre tolérance au risque et à votre stratégie d'investissement globale, TD Ameritrade peut vous aider à poursuivre vos stratégies de négociation d'options avec de puissantes plateformes de négociation, ressources de génération d'idées, et le soutien dont vous avez besoin.

En savoir plus sur les avantages et les risques potentiels de la négociation d'options.

TD Ameritrade et TFNN Corp sont séparés et non affiliés et ne sont pas responsables des services de l'autre, police, ou commentaire.