Comprendre la tarification des options
Vous avez peut-être réussi à battre le marché en négociant des actions en utilisant un processus discipliné en anticipant un bon mouvement à la hausse ou à la baisse. De nombreux traders ont également acquis la confiance nécessaire pour gagner de l'argent sur le marché boursier en identifiant un ou deux bons titres susceptibles de faire un grand pas bientôt. Mais si vous ne savez pas profiter de ce mouvement, vous pourriez être laissé dans la poussière. Si cela vous ressemble, il est peut-être temps d'envisager d'utiliser des options.
Points clés à retenir
- Les contrats d'options peuvent être évalués à l'aide de modèles mathématiques tels que les modèles de tarification Black-Scholes ou Binomial.
- Le prix d'une option est principalement composé de deux parties distinctes :sa valeur intrinsèque et sa valeur temps.
- La valeur intrinsèque est une mesure de la rentabilité d'une option basée sur le prix d'exercice par rapport au prix de l'action sur le marché.
- La valeur temps est basée sur la volatilité attendue de l'actif sous-jacent et le temps jusqu'à l'expiration de l'option.
Cet article explorera les facteurs à considérer si vous envisagez de négocier des options pour profiter des mouvements de stock. Les options sont des contrats dérivés qui donnent à leur détenteur le droit, mais pas l'obligation, acheter (dans le cas d'un call) ou vendre (dans le cas d'un put) un actif ou un titre sous-jacent à un prix prédéterminé (appelé prix d'exercice) avant l'expiration du contrat. D'où, le terme « dérivé » signifie simplement que la valeur d'une option est dérivée principalement de l'actif sous-jacent auquel elle est associée.
Il est important de noter, cependant, qu'il y a deux parties à un contrat d'option :un acheteur et un vendeur. Comme mentionné, un acheteur d'un contrat d'options a des droits, mais le vendeur d'un contrat d'options, d'autre part, a une obligation. Cela peut devenir déroutant, donc pour résumer :
- Acheteur d'un call :le droit d'acheter un actif à un prix (d'exercice) prédéterminé
- Vendeur d'un call :l'obligation de vendre un actif à un prix (d'exercice) prédéterminé
- Acheteur d'un put :le droit de vendre un actif à un prix (d'exercice) prédéterminé
- Vendeur d'un put :l'obligation d'acheter un actif à un prix (d'exercice) prédéterminé
L'achat ou la vente d'une option a un prix, appelée prime de l'option. Comprendre comment évaluer cette prime est crucial pour le trading d'options, et repose essentiellement sur la probabilité que le droit ou l'obligation d'acheter ou de vendre une action finisse par être rentable à l'expiration. Ainsi, les acheteurs d'une option paient la prime, et les vendeurs d'une option reçoivent la prime
Modèles de tarification des options
Avant de vous aventurer dans le monde du trading d'options, les investisseurs doivent avoir une bonne compréhension des facteurs déterminant la valeur d'une option. Il s'agit notamment du cours actuel de l'action, la valeur intrinsèque, le délai d'expiration ou la valeur du temps, volatilité, taux d'intérêt, et les dividendes en espèces versés.
Il existe plusieurs modèles d'évaluation des options qui utilisent ces paramètres pour déterminer la juste valeur marchande d'une option. Parmi ceux-ci, le modèle Black-Scholes est le plus connu. À bien des égards, les options sont comme n'importe quel autre investissement :vous devez comprendre ce qui détermine leur prix pour les utiliser efficacement. D'autres modèles sont également couramment utilisés, tels que le modèle binomial et le modèle trinôme.
Commençons par les principaux moteurs du prix d'une option :cours actuel de l'action, valeur intrinsèque, délai d'expiration ou valeur temporelle, et la volatilité. Le cours actuel de l'action est assez simple. Le mouvement du prix de l'action à la hausse ou à la baisse a un effet direct, bien que non égal, effet sur le prix de l'option. Lorsque le prix d'une action augmente, plus il est probable que le prix d'une option d'achat augmentera et que le prix d'une option de vente baissera. Si le cours de l'action baisse, l'inverse se produira très probablement pour le prix des options d'achat et de vente.
La formule Black-Scholes
Le modèle Black-Scholes est peut-être la méthode de tarification des options la plus connue. La formule du modèle est dérivée en multipliant le cours de l'action par la fonction de distribution de probabilité normale standard cumulative. Après, la valeur actuelle nette (VAN) du prix d'exercice multipliée par la distribution normale standard cumulée est soustraite de la valeur résultante du calcul précédent.
En notation mathématique :
C=StN(d1)−Ke−rtN(d2)où:d1=σs tlnKSt+(r+2σv2) tetd2=d1−σs t où :C=Prix de l'option d'achatS=Prix de l'action actuelle (ou autre sous-jacent)K=Prix d'exercice=Taux d'intérêt sans risquet=Durée jusqu'à l'échéanceN=Une distribution normale
Les mathématiques impliquées dans une équation différentielle qui compose la formule Black-Scholes peuvent être compliquées et intimidantes. Heureusement, vous n'avez pas besoin de connaître ou même de comprendre les mathématiques pour utiliser la modélisation Black-Scholes dans vos propres stratégies. Les traders d'options et les investisseurs ont accès à une variété de calculateurs d'options en ligne, et de nombreuses plateformes de trading d'aujourd'hui disposent d'outils d'analyse d'options robustes, y compris des indicateurs et des feuilles de calcul qui effectuent les calculs et génèrent les valeurs de tarification des options.
Au dessous de, nous allons creuser un peu plus dans les prix des options pour comprendre ce qui constitue sa valeur intrinsèque par rapport à extrinsèque (temps), ce qui est un peu plus simple.
1:23Comprendre la tarification des options
Valeur intrinsèque
La valeur intrinsèque est la valeur qu'aurait une option donnée si elle était exercée aujourd'hui. Essentiellement, la valeur intrinsèque est le montant par lequel le prix d'exercice d'une option est rentable ou dans le cours par rapport au prix de l'action sur le marché. Si le prix d'exercice de l'option n'est pas rentable par rapport au prix de l'action, l'option est dite hors de la monnaie. Si le prix d'exercice est égal au prix de l'action sur le marché, l'option est dite « à parité ».
Bien que la valeur intrinsèque comprenne la relation entre le prix d'exercice et le prix de l'action sur le marché, il ne tient pas compte du temps (ou du peu) restant jusqu'à l'expiration de l'option, appelée expiration. Le temps restant sur une option a un impact sur la prime ou la valeur d'une option, que nous explorerons dans la section suivante. En d'autres termes, la valeur intrinsèque est la partie du prix d'une option qui n'est pas perdue ou affectée par le passage du temps.
La formule et le calcul de la valeur intrinsèque
Voici les équations pour calculer la valeur intrinsèque d'une option d'achat ou de vente :
Valeur intrinsèque de l'option d'achat=USC−CSwhere :USC=Prix actuel de l'action sous-jacenteCS=Prix d'exercice de l'appel
La valeur intrinsèque d'une option reflète l'avantage financier effectif résultant de l'exercice immédiat de cette option. Essentiellement, il s'agit de la valeur minimale d'une option. Options négociées à la monnaie ou hors de la monnaie, n'ont aucune valeur intrinsèque.
Valeur intrinsèque de l'option de vente = PS−USCwhere : PS=Prix d'exercice de vente
Exemple de valeur intrinsèque
Par exemple, disons que les actions de General Electric (GE) se vendent à 34,80 $. L'option d'achat GE 30 aurait une valeur intrinsèque de 4,80 $ (34,80 $ - 30 $ =4,80 $) car le détenteur de l'option peut exercer l'option d'achat d'actions GE à 30 $, puis retournez-les et vendez-les automatiquement sur le marché pour 34,80 $ pour un profit de 4,80 $.
Dans un autre exemple, l'option d'achat GE 35 aurait une valeur intrinsèque de zéro (34,80 $ - 35 $ =-0,20 $) car la valeur intrinsèque ne peut pas être négative. La valeur intrinsèque fonctionne également de la même manière pour une option de vente.
Par exemple, une option de vente GE 30 aurait une valeur intrinsèque de zéro (30 $ - 34,80 $ =-4,80 $) car la valeur intrinsèque ne peut pas être négative. D'autre part, une option de vente GE 35 aurait une valeur intrinsèque de 0,20 $ (35 $ - 34,80 $ =0,20 $).
Valeur de temps
Étant donné que les contrats d'options ont une durée limitée avant leur expiration, le temps restant a une valeur monétaire qui lui est associée, appelée valeur temps. Il est directement lié au temps dont dispose une option jusqu'à son expiration, ainsi que la volatilité, ou des fluctuations, dans le cours de l'action.
Plus une option a de temps jusqu'à son expiration, plus il y a de chances qu'il finisse dans l'argent. La composante temporelle d'une option décroît de façon exponentielle. La dérivation réelle de la valeur temporelle d'une option est une équation assez complexe.
En règle générale, une option perdra un tiers de sa valeur pendant la première moitié de sa durée et les deux tiers pendant la seconde moitié de sa durée. Il s'agit d'un concept important pour les investisseurs en valeurs mobilières, car plus l'option approche de l'expiration, plus un mouvement du titre sous-jacent est nécessaire pour avoir un impact sur le prix de l'option.
La formule et le calcul de la valeur du temps
La formule ci-dessous montre que la valeur temps est dérivée en soustrayant la valeur intrinsèque d'une option de la prime d'option.
Valeur temporelle = Prix de l'option – Valeur intrinsèque
En d'autres termes, la valeur temps est ce qui reste de la prime après avoir calculé la rentabilité entre le prix d'exercice et le cours de l'action sur le marché. Par conséquent, La valeur temps est souvent appelée valeur extrinsèque d'une option, car la valeur temps est le montant par lequel le prix d'une option dépasse la valeur intrinsèque.
La valeur temps est essentiellement la prime de risque dont le vendeur d'options a besoin pour donner à l'acheteur d'options le droit d'acheter ou de vendre les actions jusqu'à la date d'expiration de l'option. C'est comme une prime d'assurance pour l'option; plus le risque est élevé, plus le coût d'achat de l'option est élevé.
Exemple de valeur temporelle
En reprenant l'exemple ci-dessus, si GE se négocie à 34,80 $ et que l'option d'achat GE 30 à un mois d'expiration se négocie à 5 $, la valeur temps de l'option est de 0,20 $ (5,00 $ - 4,80 $ =0,20 $).
Pendant ce temps, avec GE à 34,80 $, une option d'achat GE 30 se négociant à 6,85 $ avec neuf mois d'expiration a une valeur temporelle de 2,05 $. (6,85 $ - 4,80 $ =2,05 $). Notez que la valeur intrinsèque est la même; la différence de prix de la même option à prix d'exercice est la valeur temps.
Volatilité
La valeur temporelle d'une option dépend également fortement de la volatilité que le marché s'attend à ce que l'action affiche jusqu'à l'expiration. Typiquement, les actions à forte volatilité ont une probabilité plus élevée que l'option soit rentable ou dans le cours à l'expiration. Par conséquent, la valeur temps, en tant que composante de la prime de l'option, est généralement plus élevée pour compenser le risque accru que le prix de l'action dépasse le prix d'exercice et expire dans le cours. Pour les stocks qui ne devraient pas beaucoup bouger, la valeur temporelle de l'option sera relativement faible.
L'une des mesures utilisées pour mesurer les actions volatiles est appelée bêta. Le bêta mesure la volatilité d'une action par rapport à l'ensemble du marché. Les actions volatiles ont tendance à avoir des bêtas élevés principalement en raison de l'incertitude du prix de l'action avant l'expiration de l'option. Cependant, les actions à bêta élevé comportent également plus de risques que les actions à faible bêta. En d'autres termes, la volatilité est une arme à double tranchant, ce qui signifie qu'il permet aux investisseurs le potentiel de rendements importants, mais la volatilité peut également entraîner des pertes importantes.
L'effet de la volatilité est essentiellement subjectif et difficile à quantifier. Heureusement, il existe plusieurs calculatrices pour aider à estimer la volatilité. Pour rendre cela encore plus intéressant, plusieurs types de volatilité existent, avec implicite et historique étant le plus noté. Lorsque les investisseurs examinent la volatilité dans le passé, on l'appelle soit volatilité historique, soit volatilité statistique.
Volatilité historique
La volatilité historique (HV) vous aide à déterminer l'ampleur possible des mouvements futurs de l'action sous-jacente. Statistiquement, les deux tiers de toutes les occurrences d'un cours d'action se produiront à plus ou moins un écart type du mouvement de l'action sur une période de temps définie.
La volatilité historique remonte dans le temps pour montrer à quel point le marché a été volatil. Cela aide les investisseurs en options à déterminer quel prix d'exercice est le plus approprié pour une stratégie particulière.
La volatilité implicite
La volatilité implicite est ce qui est impliqué par les prix actuels du marché et est utilisé avec des modèles théoriques. Il aide à fixer le prix actuel d'une option existante et aide les joueurs d'options à évaluer le potentiel d'une transaction. La volatilité implicite mesure les options que les traders attendent de la volatilité future.
En tant que tel, la volatilité implicite est un indicateur du sentiment actuel du marché. Ce sentiment se reflétera dans le prix des options, aider les traders à évaluer la volatilité future de l'option et de l'action en fonction des prix actuels des options.
Collectivement, les facteurs qui aident à mesurer l'impact sur la prime d'une option sont appelés options grecques.
Exemples de tarification des options
Au dessous de, vous pouvez voir l'exemple GE déjà discuté. Il montre le prix de négociation de GE, plusieurs prix d'exercice, et les valeurs intrinsèques et temporelles des options d'achat et de vente. Au moment d'écrire ces lignes, General Electric était considérée comme une action à faible volatilité et avait un bêta de 0,49 pour cet exemple.
Le tableau ci-dessous contient les prix des appels et des options de vente qui expirent dans un mois (partie supérieure du tableau). La section inférieure contient les prix des options GE qui expirent dans neuf mois.

Dans la figure ci-dessous, les prix des appels et des options de vente expirant dans un mois et neuf mois sont répertoriés pour les actions d'Amazon.com Inc. (AMZN). Amazon est une action beaucoup plus volatile avec un bêta de 3,47.
Comparons l'option d'achat GE 35 à neuf mois d'expiration avec l'option d'achat AMZN 40 à neuf mois d'expiration.
- GE n'a que 0,20 $ pour progresser avant que l'option de neuf mois ne soit au prix, (35 $ d'exercice - 34,80 $ cours de l'action).
- D'autre part, AMZN a 1,30 $ pour augmenter avant que son option de neuf mois ne soit à la monnaie (40 $ d'exercice - cours de l'action 38,70 $).
- La valeur temporelle de ces options est de 3,70 $ pour GE et de 7,50 $ pour AMZN.
La prime importante sur l'option AMZN est due à la nature volatile du titre AMZN, ce qui pourrait augmenter la probabilité que l'option expire dans le cours.

Un vendeur d'options de GE ne s'attendra pas à obtenir une prime substantielle car les acheteurs ne s'attendent pas à ce que le prix de l'action évolue de manière significative.
D'un côté, le vendeur d'une option AMZN peut s'attendre à recevoir une prime plus élevée en raison de la nature volatile de l'action AMZN. Essentiellement, lorsque le marché estime qu'une action sera très volatile, la valeur temps de l'option augmente.
D'autre part, lorsque le marché estime qu'une action sera moins volatile, la valeur temps de l'option chute. L'attente par le marché de la volatilité future d'une action est la clé du prix des options.
Options
- Comment les contrats à terme sont-ils utilisés pour couvrir une position ?
- Comment les fonds communs de placement sont évalués
- Connaître la valeur de vos options
- Comprendre l'option Thêta
- Que sont les options binaires ?
- Comprendre l'option gamma
- Comment négocier des options
- Que sont les options d'achat d'actions et comment fonctionnent-elles ?
- Comment embaucher un planificateur financier - Comprendre leur valeur, leurs lettres de créance, et comment ils sont rémunérés
-
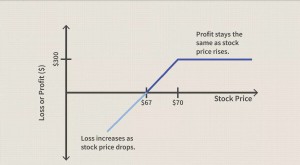 Options de vente
Options de vente Lincorporation doptions dans tous les types de stratégies dinvestissement a rapidement gagné en popularité parmi les investisseurs individuels. Pour les commerçants débutants, lune des principales que...
-
 Que sont les options :les options d'achat et de vente ?
Que sont les options :les options d'achat et de vente ? Une option est un dérivé, un contrat qui donne le droit à lacheteur, mais pas lobligation, acheter ou vendre lactif sous-jacent avant une certaine date (date dexpiration) à un prix spécifié (prix dexe...


