Qu'est-ce que le rendement composé en continu ?

Le rendement composé en continu est ce qui se produit lorsque les intérêts gagnés sur un investissement sont calculés et réinvestis dans le compte pour un nombre infini de périodes. Les intérêts sont calculés sur le montant principal et les intérêts accumulés au cours des périodes données et réinvestis dans le solde de trésorerie.

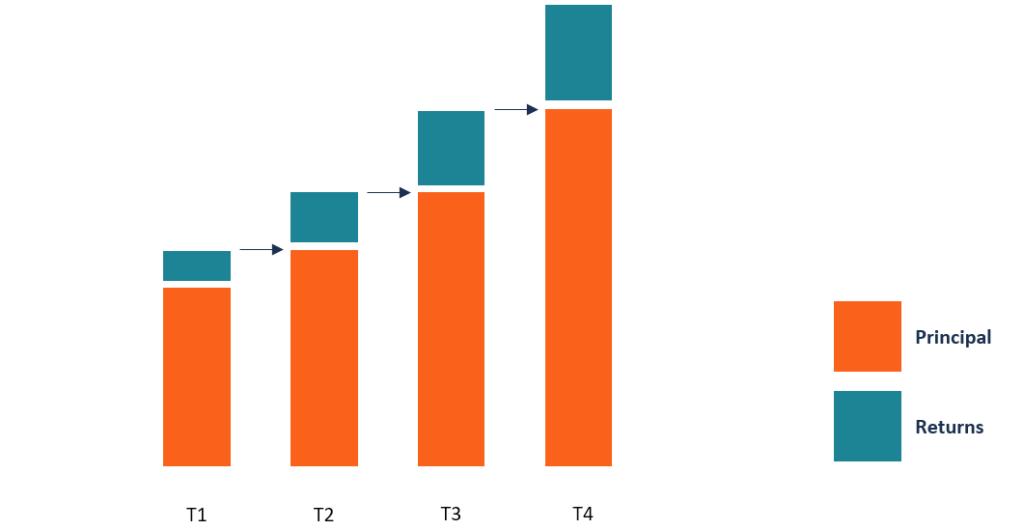
La composition régulière est calculée sur des intervalles de temps spécifiques tels que mensuels, trimestriel, semestriellement et annuellement. La composition continue est un cas extrême de ce type de composition car elle calcule les intérêts sur un nombre infini de périodes, plutôt que de supposer un nombre spécifique de périodes. La différence entre les intérêts gagnés par la méthode de composition traditionnelle et la méthode de composition continue peut être importante.

Rendement composé annuel par rapport au rendement composé en continu

Les investisseurs calculent l'intérêt ou le taux de rendementTaux de rendementLe taux de rendement (ROR) est le gain ou la perte d'un investissement sur une période de temps par rapport au coût initial de l'investissement exprimé en pourcentage. Ce guide enseigne les formules les plus courantes sur leurs investissements en utilisant deux techniques principales :la composition annuelle et la composition continue.

Composition annuelle

La composition annuelle signifie que le retour sur investissement est calculé chaque année, et c'est différent du simple intérêt. La méthode de composition annuelle utilise la formule suivante :

Total =[Principal x (1 + Intérêts)] ^Nombre d'années

Le retour sur investissement s'obtient en déduisant le montant en principal des rendements totaux obtenus à l'aide de la formule ci-dessus.

Supposons que la société ABC a investi 10 $, 000 pour acheter un instrument financier, et le taux de rendement est de 5 % pendant deux ans. Par conséquent, les intérêts gagnés sur le placement d'ABC pour la période de deux ans sont les suivants :

=[10, 000 x (1+0,05)^2

=(10, 000 x 1.1025)

=11, 025 – 10, 000

= 1 $, 025

Par conséquent, La société ABC a gagné des intérêts de 1 $, 025 sur son investissement de 10 $, 000 sur deux ans.

Rendement composé en continu

Contrairement à la composition annuelle, qui implique un nombre déterminé de périodes, le nombre de périodes utilisées pour la composition continue est infiniment nombreux. Au lieu d'utiliser le nombre d'années dans l'équation, la composition continue utilise une constante exponentielle pour représenter le nombre infini de périodes. La formule pour le capital plus les intérêts est la suivante :

Total =Principal x e^(Intérêt x Années)

Où:

• e – la fonction exponentielle, qui est égal à 2,71828.

En utilisant l'exemple de la société ABC ci-dessus, le retour sur investissement peut être calculé comme suit lors de l'utilisation de la composition continue :

=10, 000 x 2,71828^ (0,05 x 2)

=10, 000 x 1.1052

= 11,1 $ 052

Intérêt =11 $, 052 – 10 $, 000

= 1 $, 052

La différence entre le retour sur investissementRetour sur investissement (ROI)Le retour sur investissement (ROI) est une mesure de performance utilisée pour évaluer les retours sur investissement ou comparer l'efficacité de différents investissements. lors de l'utilisation de la composition continue par rapport à la composition annuelle est de 27 $ (1 $, 052 – 1025 $).

Du quotidien, Mensuel, Trimestriel, et composition semi-annuelle

Outre les méthodes de composition annuelle et continue, l'intérêt peut également être composé à différents intervalles de temps tels que quotidiennement, mensuel, trimestriellement et semestriellement.

Pour illustrer la composition à différents intervalles de temps, nous prenons un investissement initial de 1 $, 000 qui paie un taux d'intérêtTaux d'intérêtUn taux d'intérêt fait référence au montant facturé par un prêteur à un emprunteur pour toute forme de dette donnée, généralement exprimé en pourcentage du principal. de 8%.

Composition quotidienne

La formule de composition quotidienne est la suivante :

=Principal x (1+Intérêt/365)^365

=1, 000 x (1 + 0,08/365) ^ 365

=1, 000 x (1 + 0,00022)^365

=1, 000 x (1.00022) ^ 365

=1, 000 x 1,0836

= 1 $, 083.60

Composition mensuelle

La formule des intervalles mensuels est la suivante :

=Principal x (1+Intérêt/12)^12

=1, 000 x (1+0,08/12) ^12

=1, 000 x [1+0,0067)^12

=1, 000 x (1.0067)^12

=1, 000 x (1,083)

= $ 1, 083.00

Composition trimestrielle

La formule de composition trimestrielle est la suivante :

=Principal x (1 + intérêt/4)^4

=1, 000 x (1 +0,08/4)^4

=1, 000 x (1 + 0,02)^4

=1, 000 x (1,02)^4

=1, 000 x 1,0824

= 1 $, 082.40

Composition semi-annuelle

La formule de composition semestrielle est la suivante :

=Principal x (1 + intérêts/2)^2

=1, 000 x (1 + 0,08/2)^2

=1, 000 x (1 + 0,04)^2

=1, 000 x (1,04)^2

=1, 000 x 1.0816

= 1 $, 081.60

Conclusion sur les intervalles de composition

A partir des calculs ci-dessus, on peut conclure que tous les intervalles produisent un intérêt presque égal, mais avec une petite variation. Par exemple, la composition trimestrielle produit un intérêt de 82,40 $, ce qui est légèrement supérieur à l'intérêt produit par la composition semestrielle à 81,60 $.

Aussi, le taux mensuel rapporte un intérêt de 83 $, ce qui est légèrement supérieur à l'intérêt produit par les taux trimestriels à 82,40 $. La composition quotidienne donne un intérêt plus élevé de 83,60 $, ce qui est légèrement supérieur à l'intérêt au taux mensuel de 82,60 $.

À partir du modèle ci-dessus, nous pouvons également dire que les petits intervalles de composition des intérêts produisent des taux d'intérêt plus élevés que les grands intervalles de composition.

Importance du compoundage continu

La composition continue offre divers avantages par rapport à l'intérêt simpleIntérêt simpleFormule d'intérêt simple, définition et exemple. L'intérêt simple est un calcul d'intérêt qui ne tient pas compte de l'effet de la composition. Dans de nombreux cas, intérêts composés avec chaque période désignée d'un prêt, mais en cas d'intérêt simple, ce ne est pas. Le calcul de l'intérêt simple est égal au montant en principal multiplié par le taux d'intérêt, multiplié par le nombre de périodes. et composition régulière. Les avantages comprennent :

1. Réinvestir les gains perpétuellement

L'un des avantages de la composition continue est que les intérêts sont réinvestis dans le compte sur un nombre infini de périodes. Cela signifie que les investisseurs bénéficient de la croissance continue de leurs portefeuilles, par rapport au moment où ils gagnent des intérêts mensuels, trimestriel, ou annuellement avec une composition régulière.

2. Le montant des intérêts continuera d'augmenter

En mélange continu, l'intérêt et le capital ne cessent de croître, ce qui permet de multiplier plus facilement les rendements sur le long terme. D'autres formes de capitalisation ne rapportent que des intérêts sur le capital et ces intérêts sont payés au fur et à mesure qu'ils sont gagnés. Le réinvestissement des intérêts permet à l'investisseur de gagner à un taux exponentiel pour un nombre infini de périodes.

Ressources additionnelles

Merci d'avoir lu l'explication de CFI sur le rendement composé en continu. CFI propose la certification Financial Modeling &Valuation Analyst (FMVA)™ Devenez un Certified Financial Modeling &Valuation Analyst (FMVA)®. Inscrivez-vous aujourd'hui ! programme de certification pour ceux qui cherchent à faire passer leur carrière au niveau supérieur. Pour continuer à apprendre et à progresser dans votre carrière, les ressources de la FCI suivantes seront utiles :

• Taux En Pourcentage Annuel (TAEG)Taux En Pourcentage Annuel (TAEG)Le Taux En Pourcentage Annuel (TAEG) est le taux d'intérêt annuel qu'un individu doit payer sur un prêt, ou qu'ils reçoivent sur un compte de dépôt. Finalement, APR est un terme de pourcentage simple utilisé pour exprimer le montant numérique payé par un individu ou une entité chaque année pour le privilège d'emprunter de l'argent.
• Taux de croissance annuel composé (TCAC) CAGRCAGR signifie taux de croissance annuel composé. C'est une mesure du taux de croissance annuel d'un investissement dans le temps, avec prise en compte de la composition.
• Calculateur de taux d'intérêtCalculateur de taux d'intérêtCalculateur de taux d'intérêt pour vous aider à calculer le taux d'intérêt effectif en fonction du nombre de périodes, type de taux d'intérêt, et le montant du solde initial.
• Paiement du principalPaiement du principalUn paiement du principal est un paiement vers le montant initial d'un prêt qui est dû. En d'autres termes, un paiement de capital est un paiement effectué sur un prêt qui réduit le montant restant dû du prêt, plutôt que de s'appliquer au paiement des intérêts perçus sur le prêt.