Tests d'hypothèses en finance :concept et exemples

Votre conseiller en placement vous propose un plan de placement à revenu mensuel qui promet un rendement variable chaque mois. Vous n'y investirez que si vous êtes assuré d'un revenu mensuel moyen de 180 $. Votre conseiller vous dit également que depuis les 300 derniers mois, le programme avait des retours sur investissement d'une valeur moyenne de 190 $ et d'un écart type de 75 $. Faut-il investir dans ce schéma ? Les tests d'hypothèses viennent en aide à une telle prise de décision.

Points clés à retenir

• Le test d'hypothèse est un outil mathématique pour confirmer une affirmation ou une idée financière ou commerciale.
• Les tests d'hypothèses sont utiles pour les investisseurs qui tentent de décider dans quoi investir et si l'instrument est susceptible de fournir un rendement satisfaisant.
• Malgré l'existence de différentes méthodologies de test d'hypothèses, les quatre mêmes étapes sont utilisées :définir l'hypothèse, définir les critères, calculer la statistique, et arriver à une conclusion.
• Ce modèle mathématique, comme la plupart des outils et modèles statistiques, a des limites et est sujet à certaines erreurs, obligeant les investisseurs à envisager également d'autres modèles en conjonction avec celui-ci

Qu'est-ce que le test d'hypothèse ?

Le test d'hypothèse ou de signification est un modèle mathématique pour tester une allégation, idée ou hypothèse sur un paramètre d'intérêt dans un ensemble de population donné, en utilisant des données mesurées dans un ensemble d'échantillons. Les calculs sont effectués sur des échantillons sélectionnés pour recueillir des informations plus décisives sur les caractéristiques de l'ensemble de la population, qui permet un moyen systématique de tester des allégations ou des idées sur l'ensemble de données.

Voici un exemple simple :Un directeur d'école rapporte que les élèves de son école obtiennent une moyenne de 7 sur 10 aux examens. Pour tester cette « hypothèse, " nous enregistrons les notes de, disons, 30 élèves (échantillon) de l'ensemble de la population étudiante de l'école (disons 300) et calculons la moyenne de cet échantillon. Nous pouvons ensuite comparer la moyenne (calculée) de l'échantillon à la moyenne (déclarée) de la population et tenter de confirmer l'hypothèse.

Pour prendre un autre exemple, le rendement annuel d'un fonds commun de placement particulier est de 8 %. Supposons que le fonds commun de placement existe depuis 20 ans. Nous prélevons un échantillon aléatoire des rendements annuels du fonds commun de placement pour, dire, cinq ans (échantillon) et calculez sa moyenne. Nous comparons ensuite la moyenne (calculée) de l'échantillon à la moyenne (déclarée) de la population pour vérifier l'hypothèse.

Cet article suppose que les lecteurs sont familiarisés avec les concepts d'une table de distribution normale, formule, p-valeur et bases connexes des statistiques.

Différentes méthodologies existent pour tester les hypothèses, mais les quatre mêmes étapes de base sont impliquées :

Étape 1 :Définir l'hypothèse

D'habitude, la valeur déclarée (ou les statistiques de sinistre) est indiquée comme hypothèse et présumée vraie. Pour les exemples ci-dessus, l'hypothèse sera :

• Exemple A :Les élèves de l'école obtiennent une moyenne de 7 sur 10 aux examens.
• Exemple B :Le rendement annuel du fonds commun de placement est de 8 % par année.

Cette description déclarée constitue le " Hypothèse nulle (H 0 ) " et est assumé pour être vrai - la façon dont un accusé dans un procès devant jury est présumé innocent jusqu'à ce que sa culpabilité soit prouvée par les preuves présentées au tribunal. De la même manière, le test d'hypothèse commence par énoncer et supposer une « hypothèse nulle, », puis le processus détermine si l'hypothèse est susceptible d'être vraie ou fausse.

Le point important à noter est que nous testons l'hypothèse nulle car il existe un élément de doute sur sa validité. Quelle que soit l'information qui va à l'encontre de l'hypothèse nulle déclarée, Hypothèse alternative (H 1 ). Pour les exemples ci-dessus, l'hypothèse alternative sera :

• Les élèves obtiennent une moyenne de ne pas égal à 7.
• Le rendement annuel du fonds commun de placement est ne pas égal à 8 % par an.

En d'autres termes, l'hypothèse alternative est une contradiction directe de l'hypothèse nulle.

Comme dans un procès, le jury présume de l'innocence de l'accusé (hypothèse nulle). Le procureur doit prouver le contraire (hypothèse alternative). De la même manière, le chercheur doit prouver que l'hypothèse nulle est vraie ou fausse. Si le procureur ne prouve pas l'hypothèse alternative, le jury doit laisser partir l'accusé (en fondant la décision sur l'hypothèse nulle). De la même manière, si le chercheur ne parvient pas à prouver une hypothèse alternative (ou ne fait tout simplement rien), alors l'hypothèse nulle est supposée vraie.

Les critères de prise de décision doivent être basés sur certains paramètres des ensembles de données.

Étape 2 :Définir les critères

Les critères de prise de décision doivent être basés sur certains paramètres des ensembles de données et c'est là que le lien avec la distribution normale entre en jeu.

Selon le postulat statistique standard sur la distribution de l'échantillonnage, "Pour toute taille d'échantillon n, la distribution d'échantillonnage de X̅ est normale si la population X à partir de laquelle l'échantillon est tiré est normalement distribuée. D'où, les probabilités de toutes les autres moyennes d'échantillon possibles que l'on pourrait sélectionner sont normalement distribués.

Par exemple, déterminer si le rendement quotidien moyen, de toute action cotée sur le marché boursier XYZ, autour du jour de l'An est supérieur à 2%.

H 0 :Hypothèse nulle :moyenne =2%

H 1 :Hypothèse alternative :moyenne> 2% (c'est ce que nous voulons prouver)

Prenez l'échantillon (disons de 50 actions sur un total de 500) et calculez la moyenne de l'échantillon.

Pour une distribution normale, 95 % des valeurs se situent à moins de deux écarts types de la moyenne de la population. D'où, cette hypothèse de distribution normale et de limite centrale pour l'ensemble de données de l'échantillon nous permet d'établir 5 % comme niveau de signification. Cela a du sens car, sous cette hypothèse, il y a moins de 5 % de probabilité (100-95) d'obtenir des valeurs aberrantes au-delà de deux écarts types par rapport à la moyenne de la population. Selon la nature des jeux de données, d'autres niveaux de signification peuvent être pris à 1%, 5% ou 10%. Pour les calculs financiers (y compris la finance comportementale), 5% est la limite généralement acceptée. Si nous trouvons des calculs qui dépassent les deux écarts types habituels, alors nous avons un cas fort de valeurs aberrantes pour rejeter l'hypothèse nulle.

Graphiquement, il est représenté comme suit :

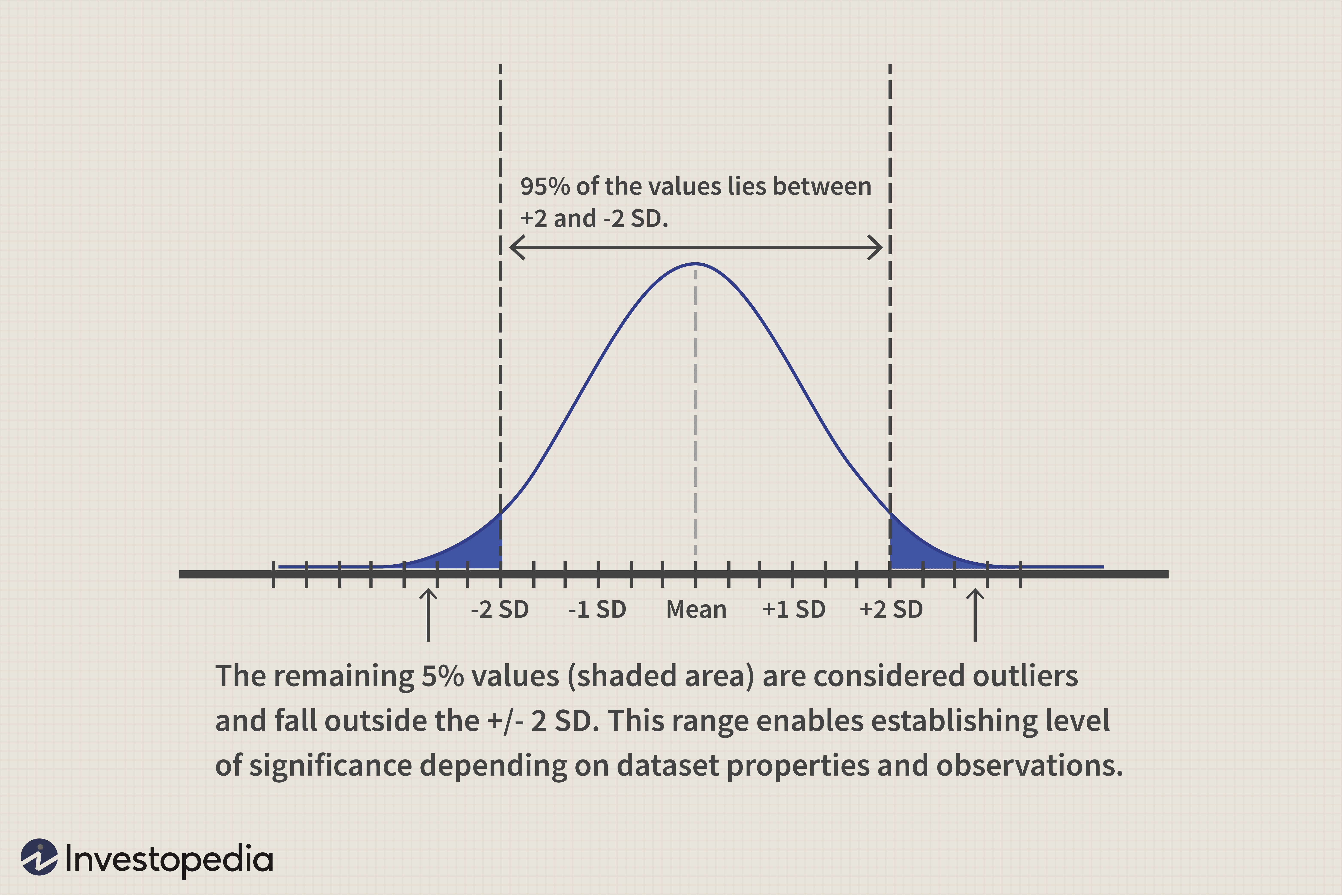
Dans l'exemple ci-dessus, si la moyenne de l'échantillon est bien supérieure à 2% (disons 3,5%), alors nous rejetons l'hypothèse nulle. L'hypothèse alternative (moyenne>2%) est acceptée, ce qui confirme que le rendement quotidien moyen des actions est bien supérieur à 2%.

Cependant, si la moyenne de l'échantillon n'est pas susceptible d'être significativement supérieure à 2 % (et reste à, dire, environ 2,2%, alors nous NE POUVONS PAS rejeter l'hypothèse nulle. Le défi est de savoir comment trancher des cas aussi rapprochés. Pour tirer une conclusion à partir d'échantillons et de résultats sélectionnés, un niveau de signification est à déterminer, ce qui permet de conclure sur l'hypothèse nulle. L'hypothèse alternative permet d'établir le niveau de signification ou le concept de « valeur critique » pour décider de ces cas à courte distance.

Selon la définition standard du manuel, « Une valeur critique est une valeur seuil qui définit les limites au-delà desquelles moins de 5 % des moyennes de l'échantillon peuvent être obtenues si l'hypothèse nulle est vraie. Les moyennes d'échantillon obtenues au-delà d'une valeur critique entraîneront une décision de rejeter l'hypothèse nulle." Dans l'exemple ci-dessus, si nous avons défini la valeur critique à 2,1%, et la moyenne calculée est de 2,2%, alors nous rejetons l'hypothèse nulle. Une valeur critique établit une démarcation claire concernant l'acceptation ou le rejet.

Étape 3 :Calculer la statistique

Cette étape consiste à calculer le(s) chiffre(s) requis, appelées statistiques de test (comme la moyenne, score z, valeur p, etc.), pour l'échantillon sélectionné. (Nous y reviendrons dans une section ultérieure.)

Étape 4 :parvenir à une conclusion

Avec la ou les valeurs calculées, décider de l'hypothèse nulle. Si la probabilité d'obtenir une moyenne d'échantillon est inférieure à 5 %, alors la conclusion est de rejeter l'hypothèse nulle. Autrement, J'accepte et conserver l'hypothèse nulle.

Types d'erreurs

Il peut y avoir quatre résultats possibles dans la prise de décision basée sur des échantillons, en ce qui concerne l'applicabilité correcte à l'ensemble de la population :

Les cas « corrects » sont ceux où les décisions prises sur les échantillons sont réellement applicables à l'ensemble de la population. Les cas d'erreurs surviennent lorsqu'on décide de retenir (ou de rejeter) l'hypothèse nulle sur la base des calculs de l'échantillon, mais cette décision ne s'applique pas vraiment à l'ensemble de la population. Ces cas constituent des erreurs de type 1 (alpha) et de type 2 (beta), comme indiqué dans le tableau ci-dessus.

La sélection de la valeur critique correcte permet d'éliminer les erreurs alpha de type 1 ou de les limiter à une plage acceptable.

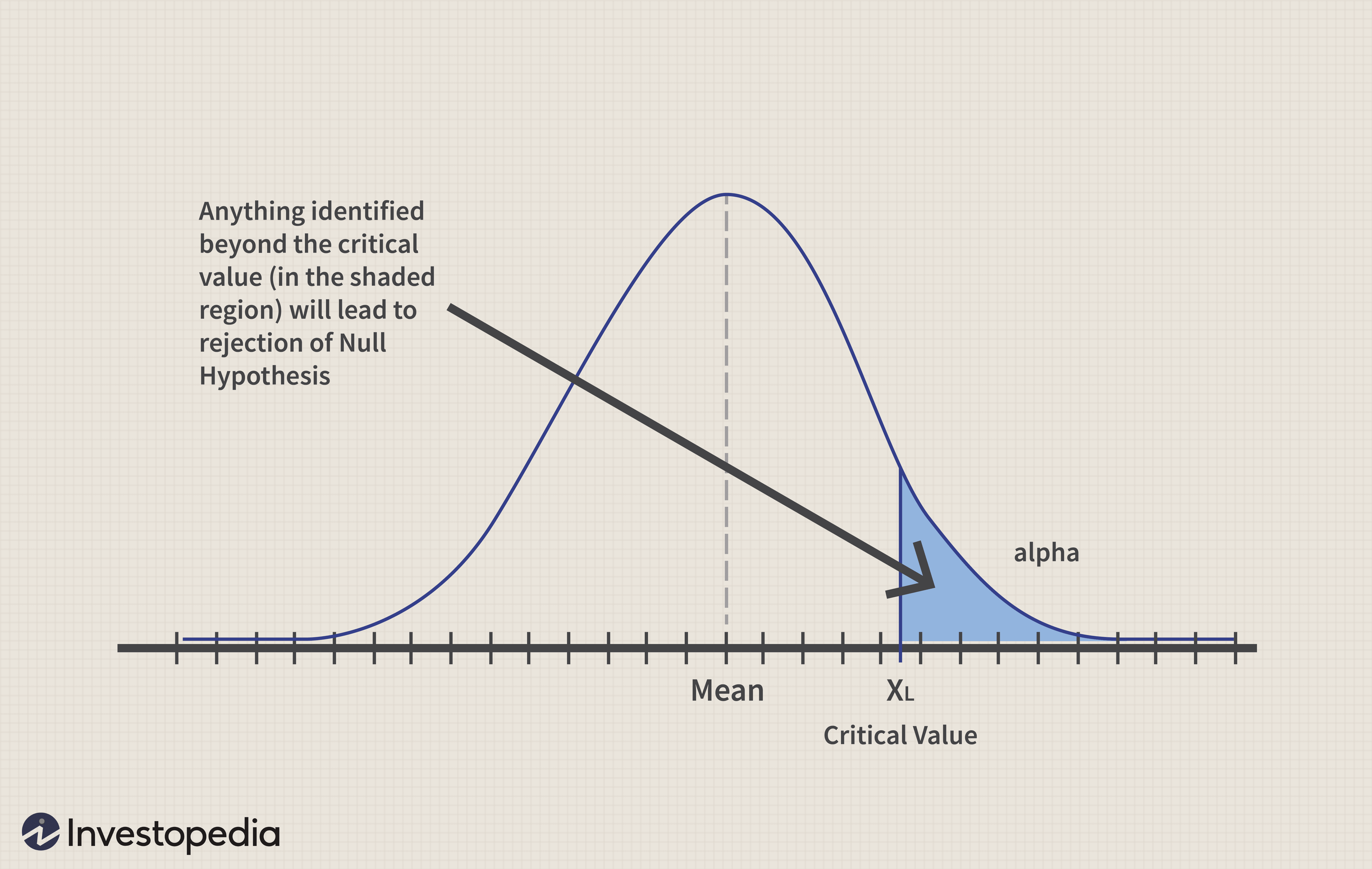
Alpha désigne l'erreur sur le niveau de signification et est déterminé par le chercheur. Pour maintenir le niveau de signification ou de confiance standard de 5 % pour les calculs de probabilité, celui-ci est retenu à 5%.

Selon les référentiels décisionnels et définitions applicables :

• « Ce critère (alpha) est généralement fixé à 0,05 (a =0,05), et nous comparons le niveau alpha à la valeur p. Lorsque la probabilité d'une erreur de type I est inférieure à 5% (p <0,05), on décide de rejeter l'hypothèse nulle; autrement, nous retenons l'hypothèse nulle.
• Le terme technique utilisé pour cette probabilité est le valeur p . Elle est définie comme « la probabilité d'obtenir un résultat d'échantillon, étant donné que la valeur indiquée dans l'hypothèse nulle est vraie. La valeur p pour l'obtention d'un résultat d'échantillon est comparée au niveau de signification."
• Une erreur de type II, ou erreur bêta, est définie comme la probabilité de retenir à tort l'hypothèse nulle, alors qu'en fait, il n'est pas applicable à l'ensemble de la population.

Quelques autres exemples montreront ceci et d'autres calculs.

Exemple 1

Il existe un programme d'investissement à revenu mensuel qui promet des rendements mensuels variables. Un investisseur n'y investira que s'il est assuré d'un revenu mensuel moyen de 180 $. L'investisseur dispose d'un échantillon de rendements sur 300 mois qui a une moyenne de 190 $ et un écart type de 75 $. Devraient-ils investir dans ce régime?

Posons le problème. L'investisseur investira dans le programme s'il est assuré du rendement moyen souhaité de 180 $ par l'investisseur.

H 0 :Null Hypothèse :moyenne =180

H 1 :Hypothèse alternative :moyenne> 180

Méthode 1 : Approche de la valeur critique

Identifier une valeur critique X L pour la moyenne de l'échantillon, qui est suffisamment grand pour rejeter l'hypothèse nulle - c'est-à-dire rejeter l'hypothèse nulle si la moyenne de l'échantillon>=valeur critique X L

P (identifier une erreur alpha de Type I) =P(rejeter H 0 étant donné que H 0 est vrai),

Ceci serait atteint lorsque la moyenne de l'échantillon dépasse les limites critiques.

=P (étant donné que H 0 est vrai) =alpha

Graphiquement, il apparaît comme suit :

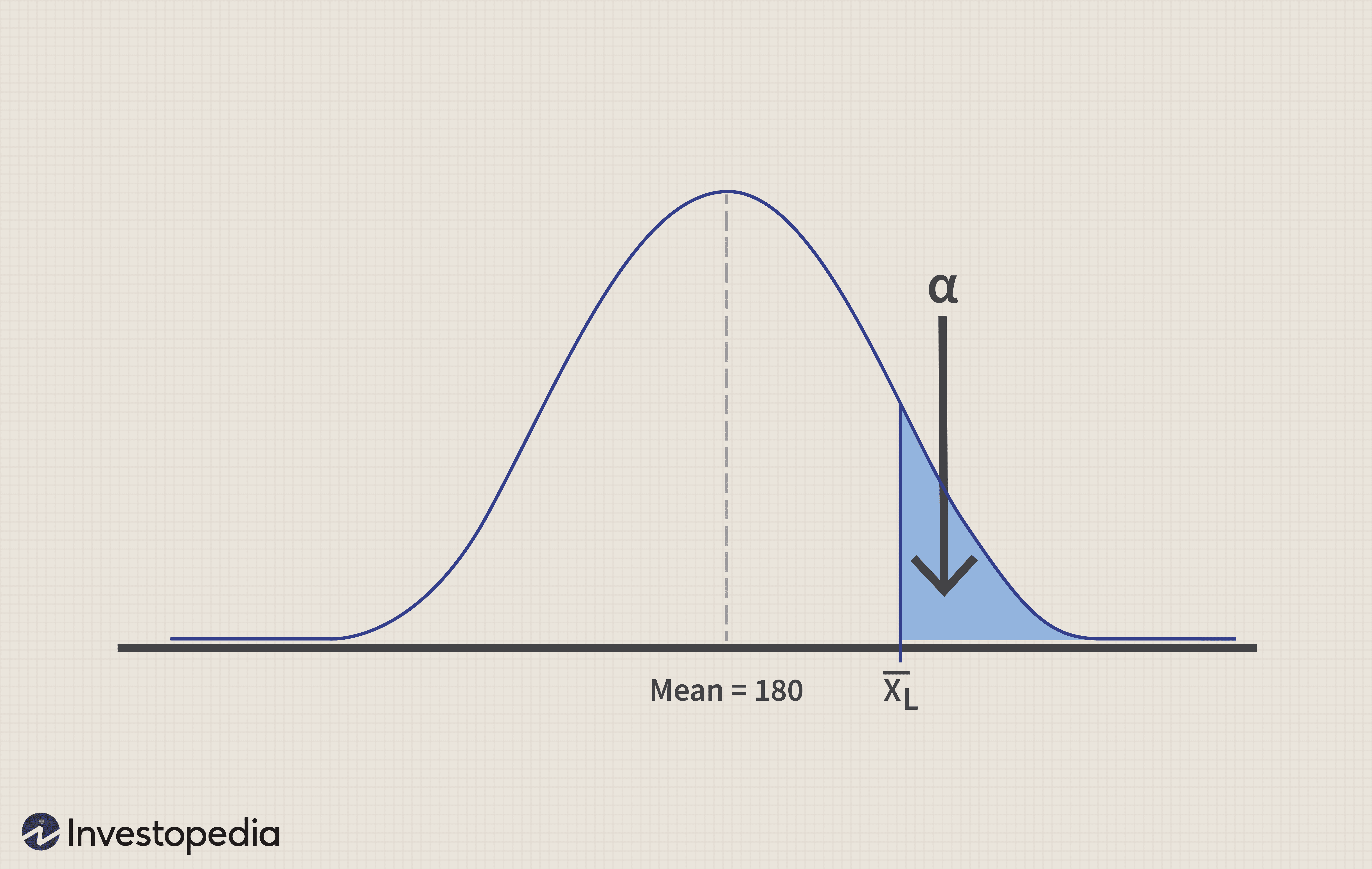
En prenant alpha =0,05 (soit un niveau de signification de 5%), Z 0,05 =1,645 (à partir de la table Z ou de la table de distribution normale)

=> X L =180 +1,645*(75/sqrt(300)) =187,12

Puisque la moyenne de l'échantillon (190) est supérieure à la valeur critique (187.12), l'hypothèse nulle est rejetée, et la conclusion est que le rendement mensuel moyen est en effet supérieur à 180 $, afin que l'investisseur puisse envisager d'investir dans ce régime.

Méthode 2 : Utilisation des statistiques de test standardisées

On peut aussi utiliser la valeur normalisée z.

Statistique de test, Z =(moyenne de l'échantillon – moyenne de la population) / (std-dev / sqrt (nombre d'échantillons).

Puis, la région de rejet devient la suivante :

Z=(190 – 180) / (75 / carré (300)) =2.309

Notre région de rejet au niveau de signification de 5% est Z> Z 0,05 =1,645.

Puisque Z=2,309 est supérieur à 1,645, l'hypothèse nulle peut être rejetée avec une conclusion similaire mentionnée ci-dessus.

Méthode 3 : calcul de la valeur P

Nous visons à identifier P (moyenne de l'échantillon>=190, lorsque moyenne =180).

=P (Z>=(190- 180) / (75 / sqrt (300))

=P (Z>=2,309) =0,0084 =0,84%

Le tableau suivant pour déduire les calculs de la valeur p conclut qu'il existe des preuves confirmées de rendements mensuels moyens supérieurs à 180 :

valeur p

Inférence

Moins que 1%

Preuve confirmée hypothèse alternative à l'appui

entre 1% et 5%

Forte évidence hypothèse alternative à l'appui

entre 5% et 10%

Faibles preuves hypothèse alternative à l'appui

supérieur à 10 %

Aucune preuve hypothèse alternative à l'appui

Exemple 2

Un nouveau courtier en valeurs mobilières (XYZ) prétend que ses frais de courtage sont inférieurs à ceux de votre courtier en valeurs mobilières actuel (ABC). Les données disponibles auprès d'un cabinet de recherche indépendant indiquent que la moyenne et le std-dev de tous les clients courtiers ABC sont de 18 $ et 6 $, respectivement.

Un échantillon de 100 clients d'ABC est prélevé et les frais de courtage sont calculés avec les nouveaux tarifs du courtier XYZ. Si la moyenne de l'échantillon est de 18,75 $ et que std-dev est le même (6 $), peut-on en déduire la différence de la facture de courtage moyenne entre les courtiers ABC et XYZ ?

H 0 :nulle Hypothèse :moyenne =18

H 1 :Hypothèse alternative :moyenne <> 18 (C'est ce que nous voulons prouver.)

Région de rejet :Z <=- Z 2.5 et Z>=Z 2.5 (en supposant un niveau de signification de 5 %, divisé 2,5 chacun de chaque côté).

Z =(moyenne de l'échantillon - moyenne) / (std-dev / sqrt (nombre d'échantillons))

=(18,75 – 18) / (6/(carré (100)) =1,25

Cette valeur Z calculée se situe entre les deux limites définies par :

-Z 2.5 =-1,96 et Z 2.5 =1,96.

Cela conclut qu'il n'y a pas suffisamment de preuves pour déduire qu'il existe une différence entre les tarifs de votre courtier existant et le nouveau courtier.

Alternativement, La valeur p =P(Z<-1,25)+P(Z>1,25)

=2 * 0,1056 =0,2112 =21,12 % ce qui est supérieur à 0,05 ou 5 %, aboutissant à la même conclusion.

Graphiquement, il est représenté par ce qui suit :

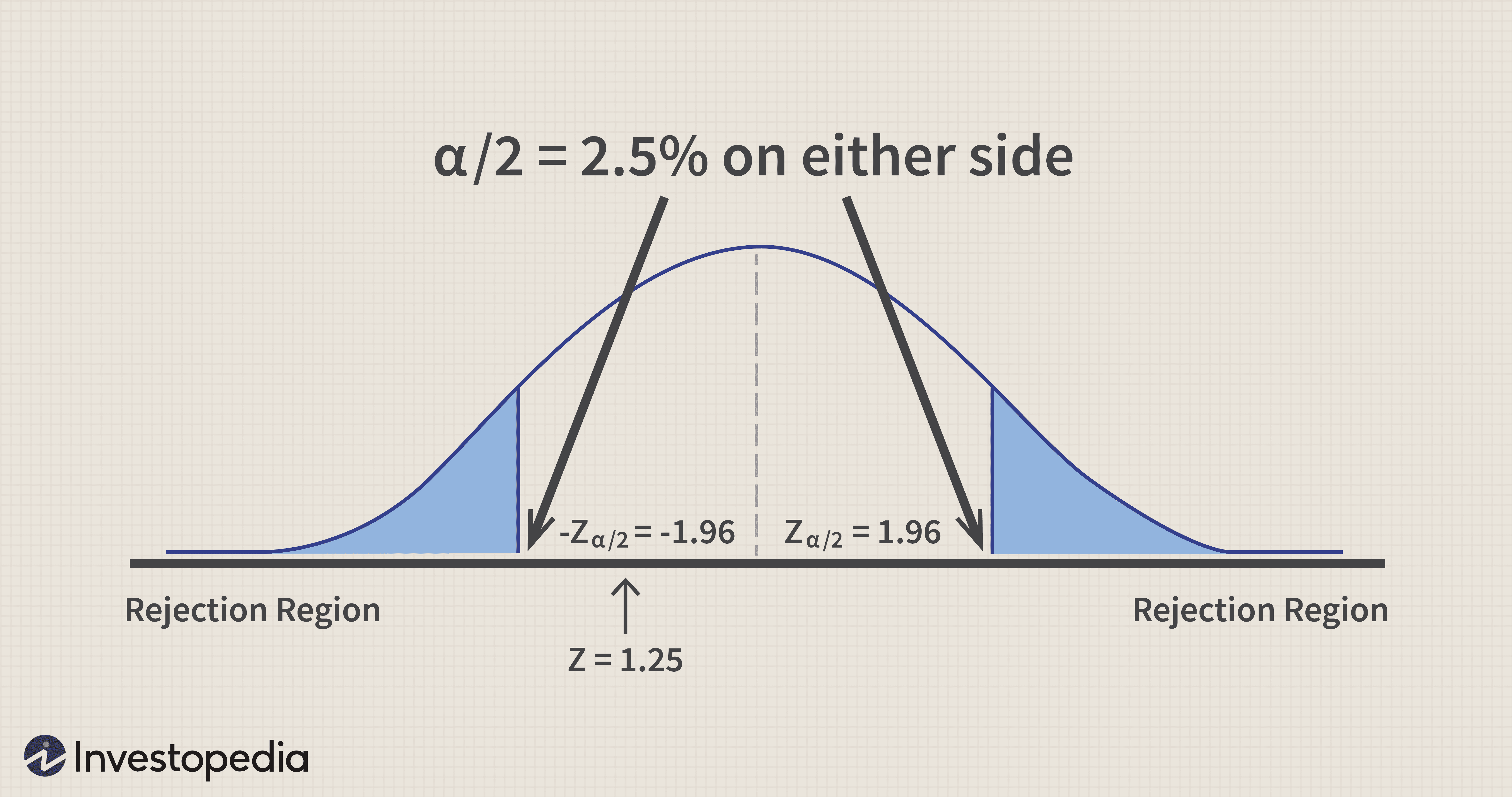
Points critiques pour la méthode de test hypothétique :

• Une méthode statistique basée sur des hypothèses
• Sujet aux erreurs comme détaillé en termes d'erreurs alpha et bêta
• L'interprétation de la valeur p peut être ambiguë, conduisant à des résultats confus

La ligne de fond

Les tests d'hypothèse permettent à un modèle mathématique de valider une affirmation ou une idée avec un certain niveau de confiance. Cependant, comme la plupart des outils et modèles statistiques, il est lié par quelques limitations. L'utilisation de ce modèle pour prendre des décisions financières doit être considérée avec un œil critique, en gardant toutes les dépendances à l'esprit. Des méthodes alternatives telles que l'inférence bayésienne valent également la peine d'être explorées pour une analyse similaire.