Qu'est-ce que la durée modifiée ?
Durée modifiée, une formule couramment utilisée dans les évaluations des obligations, exprime la variation de la valeur d'un titre en raison d'une variation des taux d'intérêtTaux d'intérêt flottantUn taux d'intérêt flottant fait référence à un taux d'intérêt variable qui évolue sur la durée de la dette. C'est le contraire d'un taux fixe. En d'autres termes, il illustre l'effet d'une variation de 100 points de base (1 %) des taux d'intérêt sur le prix d'une obligation.
La duration modifiée illustre le concept selon lequel les prix des obligations et les taux d'intérêt évoluent dans des directions opposées :des taux d'intérêt plus élevés font baisser les prix des obligations, et la baisse des taux d'intérêt fait monter les prix des obligations.
Formule pour la durée modifiée
La formule de la durée modifiée est la suivante :
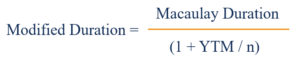
Où:
- Durée de Macaulay est le nombre moyen pondéré d'années pendant lesquelles un investisseur doit maintenir sa position dans l'obligation où la valeur actuelle (VA) du flux de trésorerie de l'obligation est égale au montant payé pour l'obligation. En d'autres termes, c'est le temps qu'il faudrait à un investisseur pour récupérer l'argent initialement investi dans l'obligation
- YTM signifie Rendement à l'Échéance. Rendement à l'Échéance (YTM) et est le rendement total d'une obligation si elle est détenue jusqu'à l'échéance
- m est le nombre de périodes de coupon par an.
Comprendre la durée de Macaulay
Pour arriver à la durée modifiée d'une obligation, il est important de comprendre le composant numérateur - la durée de Macaulay - dans la formule de durée modifiée.
La durée de Macaulay est la moyenne pondérée du temps jusqu'à ce que les flux de trésorerie d'une obligation soient reçus. En termes simples, les mesures de durée de Macaulay, dans des années, le temps nécessaire pour qu'un investisseur soit remboursé de son investissement initial dans une obligation. Une obligation avec une duration Macaulay plus élevée sera plus sensible aux variations des taux d'intérêt.
La formule pour la durée de Macaulay est la suivante :
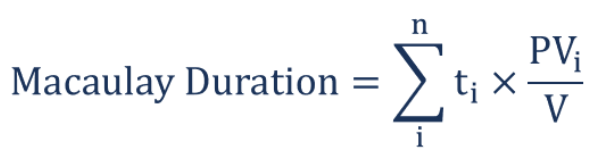
Où:
- t
je est la période - PV
je est la valeur actuelle des flux de trésorerie pondérés dans le temps - V est la valeur actuelle de tous les flux de trésorerie.
Vous trouverez ci-dessous un exemple de calcul de la durée de Macaulay sur une obligation.
Exemple de durée de Macaulay
Tim détient une obligation de 5 ans d'une valeur nominale de 1 $, 000 et un taux de coupon annuelTaux de couponUn taux de coupon est le montant des revenus d'intérêts annuels payés à un détenteur d'obligations, sur la base de la valeur nominale de l'obligation. de 5%. Le taux d'intérêt actuel est de 7%, et Tim aimerait déterminer la durée Macaulay de l'obligation. Le calcul est donné ci-dessous :

La durée de Macaulay pour l'obligation de 5 ans est calculée comme 4152,27 $ / 918,00 $ = 4,52 ans .
Mettre ensemble
Maintenant que nous comprenons et savons calculer la durée de Macaulay, nous pouvons déterminer la durée modifiée.
En utilisant l'exemple ci-dessus, on insère simplement les chiffres dans la formule pour déterminer la durée modifiée :
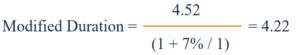
La durée modifiée est 4.22 .
Interprétation de la durée modifiée
Comment interpréter le résultat ci-dessus ? Rappelons que la duration modifiée illustre l'effet d'une variation de 100 points de base (1 %) des taux d'intérêt sur le prix d'une obligation.
Par conséquent,
- Si les taux d'intérêt augmenter de 1%, le prix de l'obligation à 5 ans sera diminuer de 4,22%.
- Si les taux d'intérêt diminuer de 1%, le prix de l'obligation à 5 ans sera augmenter de 4,22%.
La duration modifiée fournit une bonne mesure de la sensibilité d'une obligation aux variations des taux d'intérêt. Plus la duration Macaulay d'une obligation est élevée, plus la durée modifiée et la volatilité des taux d'intérêt qui en résultent sont élevées.
Ressources additionnelles
CFI est le fournisseur officiel de la certification mondiale Financial Modeling &Valuation Analyst (FMVA)™ Devenez un Certified Financial Modeling &Valuation Analyst (FMVA)®La certification Financial Modeling and Valuation Analyst (FMVA)® de CFI vous aidera à gagner la confiance dont vous avez besoin dans votre carrière financière. Inscrivez-vous aujourd'hui ! programme de certification, conçu pour aider quiconque à devenir un analyste financier de classe mondiale. Pour continuer à faire avancer votre carrière, les ressources supplémentaires ci-dessous vous seront utiles :
- Bond PricingBond PricingBond Pricing est la science du calcul du prix d'émission d'une obligation sur la base du coupon, valeur nominale, rendement et durée jusqu'à l'échéance. La tarification des obligations permet aux investisseurs
- Effective DurationEffective DurationEffective Duration est la sensibilité du prix d'une obligation par rapport à la courbe de rendement de référence. Une façon d'évaluer le risque d'une obligation consiste à estimer le
- Fonction DURÉE dans Excel Fonction DURÉE La fonction DURÉE est classée dans les fonctions financières d'Excel. Il aide à calculer la durée de Macauley. La fonction calcule la durée d'un titre qui paie des intérêts sur une base périodique avec une valeur nominale de 100 $.
- Actions vs Fixed IncomeEquity vs Fixed IncomeEquity vs Fixed Income. Les produits d'actions et de titres à revenu fixe sont des instruments financiers qui présentent des différences très importantes que tout analyste financier devrait connaître. Les investissements en actions sont généralement constitués d'actions ou de fonds d'actions, tandis que les titres à revenu fixe sont généralement constitués d'obligations de sociétés ou d'État.
investir
-
 Comment obtenir un prêt retraite
Comment obtenir un prêt retraite Lemployé de lÉtat remplit une demande de prêt de pension. Lobtention dun prêt de pension est un moyen facile pour un employé demprunter de largent contre ses cotisations acquises. Un régime de retrai...
-
 Amazon acceptera-t-il les paiements Bitcoin ?
Amazon acceptera-t-il les paiements Bitcoin ? Beaucoup ou tous les produits ici proviennent de nos partenaires qui nous paient une commission. Cest comme ça quon gagne de largent. Mais notre intégrité éditoriale garantit que les opinions de nos e...
-
 Comment se situe votre taux de prêt personnel par rapport à la moyenne ?
Comment se situe votre taux de prêt personnel par rapport à la moyenne ? Beaucoup ou tous les produits ici proviennent de nos partenaires qui nous paient une commission. Cest comme ça quon gagne de largent. Mais notre intégrité éditoriale garantit que les opinions de nos e...
-
Les conversions Roth IRA sont plus attrayantes que jamais grâce au SECURE Act
La loi SECURE récemment adoptée a changé le paysage de la retraite, nuire à lattractivité des IRA hérités pour de nombreuses personnes. Mais les changements juridiques rendent en fait plus favorable –...