Définition de la relation linéaire
Qu'est-ce qu'une relation linéaire ?
Une relation linéaire (ou association linéaire) est un terme statistique utilisé pour décrire une relation linéaire entre deux variables. Les relations linéaires peuvent être exprimées soit sous un format graphique où la variable et la constante sont reliées par une ligne droite, soit sous un format mathématique où la variable indépendante est multipliée par le coefficient de pente, ajouté par une constante, qui détermine la variable dépendante.
Une relation linéaire peut être opposée à une relation polynomiale ou non linéaire (courbe).
Points clés à retenir
- Une relation linéaire (ou association linéaire) est un terme statistique utilisé pour décrire une relation linéaire entre deux variables.
- Les relations linéaires peuvent être exprimées sous forme graphique ou sous forme d'équation mathématique de la forme y =mx + b.
- Les relations linéaires sont assez courantes dans la vie quotidienne.
L'équation linéaire est :
Mathématiquement, une relation linéaire est celle qui satisfait l'équation :
y=mx+bwhere:m=slopeb=y-intercept
Dans cette équation, "x" et "y" sont deux variables qui sont liées par les paramètres "m" et "b". Graphiquement, y =mx + b est tracé dans le plan x-y sous la forme d'une ligne de pente "m" et d'ordonnée à l'origine "b". L'ordonnée à l'origine « b » est simplement la valeur de « y » lorsque x=0. La pente « m » est calculée à partir de deux points individuels (x
m=(x2−x1)(y2−y1)
1:02Relation linéaire
Que vous dit une relation linéaire ?
Il y a trois ensembles de critères nécessaires qu'une équation doit remplir pour être qualifiée de linéaire :une équation exprimant une relation linéaire ne peut pas comprendre plus de deux variables, toutes les variables d'une équation doivent être à la puissance première, et l'équation doit représenter une ligne droite.
Une relation linéaire couramment utilisée est une corrélation, qui décrit à quel point une variable change de manière linéaire par rapport aux changements d'une autre variable.
En économétrie, la régression linéaire est une méthode souvent utilisée pour générer des relations linéaires pour expliquer divers phénomènes. Il est couramment utilisé pour extrapoler des événements du passé pour faire des prévisions pour l'avenir. Toutes les relations ne sont pas linéaires, toutefois. Certaines données décrivent des relations courbes (telles que des relations polynomiales) alors que d'autres données ne peuvent pas être paramétrées.
Fonctions linéaires
Mathématiquement similaire à une relation linéaire est le concept de fonction linéaire. Dans une variable, une fonction linéaire peut s'écrire comme suit :
f(x)=mx+bwhere:m=slopeb=y-intercept
Ceci est identique à la formule donnée pour une relation linéaire, sauf que le symbole f(x) est utilisé à la place de y. Cette substitution est faite pour mettre en évidence le sens que x est mappé à f(x), considérant que l'utilisation de oui indique simplement que x et y sont deux quantités, liés par A et B.
Dans l'étude de l'algèbre linéaire, les propriétés des fonctions linéaires sont largement étudiées et rendues rigoureuses. Étant donné un scalaire C et deux vecteurs A et B de R N , la définition la plus générale d'une fonction linéaire stipule que : c×f(A+B)=c×f(A)+c×f(B)
Exemples de relations linéaires
Exemple 1
Les relations linéaires sont assez courantes dans la vie quotidienne. Prenons le concept de vitesse par exemple. La formule que nous utilisons pour calculer la vitesse est la suivante :le taux de vitesse est la distance parcourue dans le temps. Si quelqu'un dans une mini-fourgonnette Chrysler Town and Country blanche voyage entre Sacramento et Marysville en Californie, un tronçon de 41,3 milles sur l'autoroute 99, et la fin du trajet prend 40 minutes, elle aura voyagé juste en dessous de 60 mph.
Bien qu'il y ait plus de deux variables dans cette équation, c'est toujours une équation linéaire car l'une des variables sera toujours une constante (distance).
Exemple 2
Une relation linéaire peut également être trouvée dans l'équation distance =vitesse x temps. Parce que la distance est un nombre positif (dans la plupart des cas), cette relation linéaire serait exprimée dans le quadrant supérieur droit d'un graphique avec un axe X et Y.
Si un vélo fait pour deux roulait à une vitesse de 30 milles à l'heure pendant 20 heures, le coureur finira par parcourir 600 milles. Représenté graphiquement avec la distance sur l'axe Y et le temps sur l'axe X, une ligne suivant la distance sur ces 20 heures partirait directement de la convergence des axes X et Y.
Exemple 3
Pour convertir Celsius en Fahrenheit, ou Fahrenheit à Celsius, vous utiliseriez les équations ci-dessous. Ces équations expriment une relation linéaire sur un graphique :
°C=95(°F−32)
°F=59°C+32
Exemple 4
Supposons que la variable indépendante est la taille d'une maison (mesurée en pieds carrés) qui détermine le prix du marché d'une maison (la variable dépendante) lorsqu'elle est multipliée par le coefficient de pente de 207,65 et est ensuite ajoutée au terme constant 10 $ , 500. Si la superficie d'une maison est de 1, 250 alors la valeur marchande de la maison est (1, 250 x 207,65) + 10 $, 500 =270 $, 062.50. Graphiquement, et mathématiquement, il se présente comme suit :
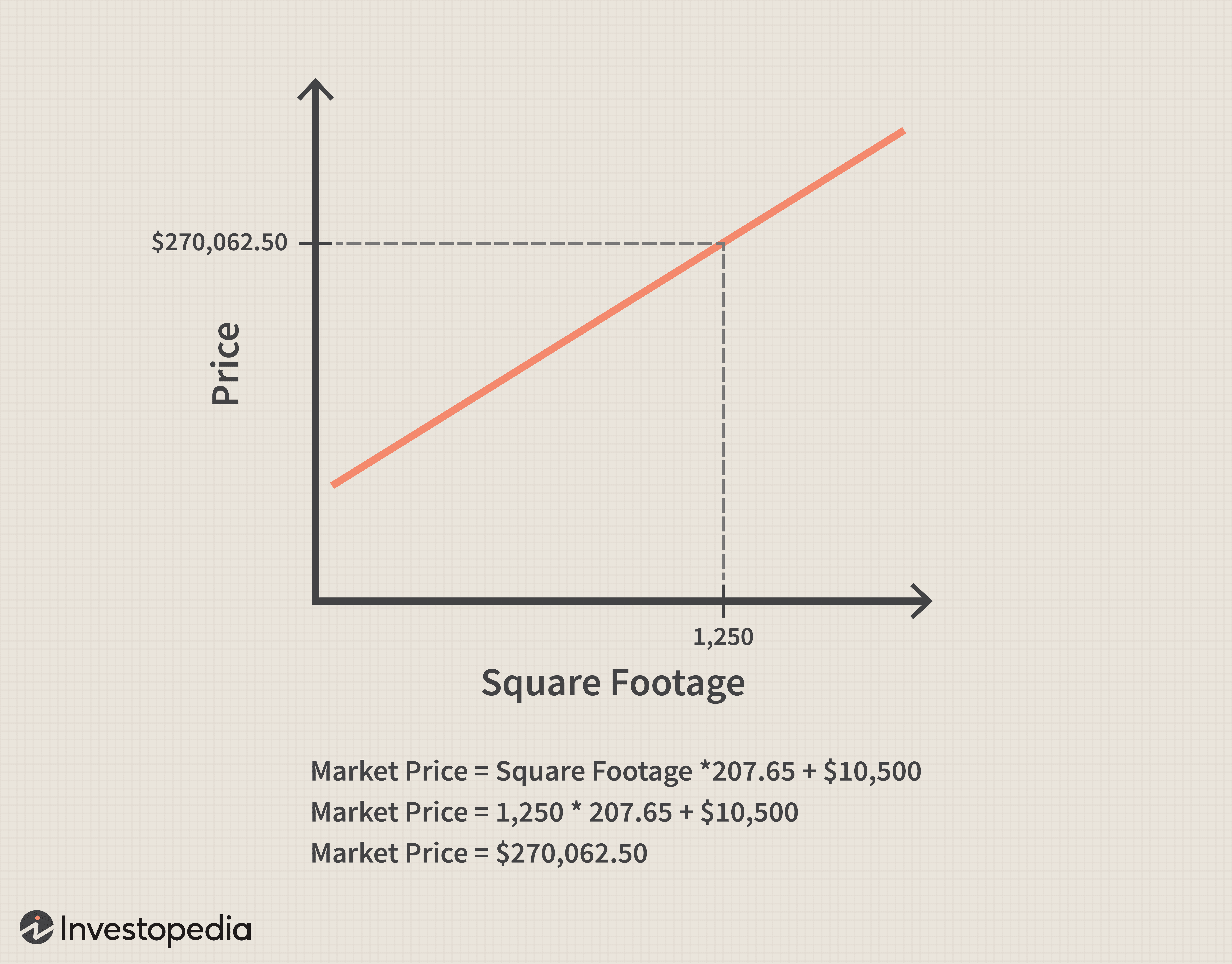
Dans cet exemple, à mesure que la taille de la maison augmente, la valeur marchande de la maison augmente de façon linéaire.
Certaines relations linéaires entre deux objets peuvent être appelées "relation proportionnelle". Cette relation apparaît comme
Y=k×Xoù :k=constantY, X=quantités proportionnelles
Lors de l'analyse des données comportementales, il existe rarement une relation linéaire parfaite entre les variables. Cependant, les lignes de tendance peuvent être trouvées dans les données qui forment une version approximative d'une relation linéaire. Par exemple, vous pouvez considérer les ventes quotidiennes de crème glacée et la température quotidienne élevée comme les deux variables en jeu dans un graphique et trouver une relation linéaire brute entre les deux.
la finance
- Définition de la prise en charge de la dette
- Définition de la moyenne géométrique
- Définition de l'évaluation
- Définition du théorème de Bayes
- Définition et explication de la garantie
- Une définition des temps d'intérêt gagnés
- Liquidité - Définition &Ratios
- Définition et explication des décaissements
- Fiduciaire - Définition &Responsabilité
-
 Qu'est-ce que l'analyse de régression ?
Qu'est-ce que l'analyse de régression ? Lanalyse de régression est un ensemble de méthodes statistiques utilisées pour lestimation des relations entre une variable dépendante et une ou plusieurs variables indépendantesVariable indépendanteU...
-
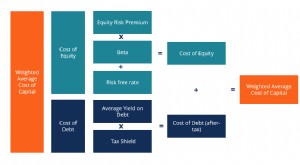 Définition du WACC
Définition du WACC Le coût moyen pondéré du capital (WACC) dune entreprise représente son coût combiné du capital. Coût du capital Le coût du capital est le taux de rendement minimum quune entreprise doit gagner avant d...