Définition du théorème de Bayes
Qu'est-ce que le théorème de Bayes ?
théorème de Bayes, du nom du mathématicien britannique du XVIIIe siècle Thomas Bayes, est une formule mathématique pour déterminer la probabilité conditionnelle. La probabilité conditionnelle est la probabilité qu'un résultat se produise, sur la base d'un résultat antérieur qui s'est produit. Le théorème de Bayes fournit un moyen de réviser les prédictions ou théories existantes (probabilités de mise à jour) compte tenu de preuves nouvelles ou supplémentaires. En finance, Le théorème de Bayes peut être utilisé pour évaluer le risque de prêter de l'argent à des emprunteurs potentiels.
Le théorème de Bayes est également appelé règle de Bayes ou loi de Bayes et constitue le fondement du domaine des statistiques bayésiennes.
Points clés à retenir
- Le théorème de Bayes vous permet de mettre à jour les probabilités prédites d'un événement en incorporant de nouvelles informations.
- Le théorème de Bayes a été nommé d'après le mathématicien du XVIIIe siècle Thomas Bayes.
- Il est souvent utilisé en finance pour actualiser l'évaluation des risques.
Comprendre le théorème de Bayes
Les applications du théorème sont très répandues et ne se limitent pas au domaine financier. Par exemple, Le théorème de Bayes peut être utilisé pour déterminer l'exactitude des résultats des tests médicaux en tenant compte de la probabilité qu'une personne donnée soit atteinte d'une maladie et de l'exactitude générale du test. Le théorème de Bayes repose sur l'incorporation de distributions de probabilités a priori afin de générer des probabilités postérieures. probabilité a priori, en inférence statistique bayésienne, est la probabilité d'un événement avant que de nouvelles données ne soient collectées. Il s'agit de la meilleure évaluation rationnelle de la probabilité d'un résultat sur la base des connaissances actuelles avant la réalisation d'une expérience. La probabilité postérieure est la probabilité révisée qu'un événement se produise après avoir pris en considération de nouvelles informations. La probabilité postérieure est calculée en mettant à jour la probabilité antérieure en utilisant le théorème de Bayes. En termes statistiques, la probabilité postérieure est la probabilité que l'événement A se produise étant donné que l'événement B s'est produit.
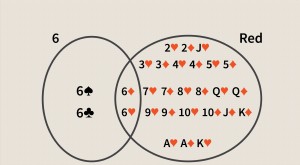
Le théorème de Bayes donne ainsi la probabilité d'un événement sur la base de nouvelles informations, c'est-à-dire ou peut être lié, à cet événement. La formule peut également être utilisée pour voir comment la probabilité qu'un événement se produise est affectée par de nouvelles informations hypothétiques, en supposant que les nouvelles informations s'avèrent vraies. Par exemple, disons qu'une seule carte est tirée d'un jeu complet de 52 cartes. La probabilité que la carte soit un roi est quatre divisée par 52, ce qui équivaut à 1/13 ou environ 7,69 %. N'oubliez pas qu'il y a quatre rois dans le deck. Maintenant, supposons qu'il soit révélé que la carte sélectionnée est une figure. La probabilité que la carte sélectionnée soit un roi, étant donné que c'est une carte de visage, est quatre divisé par 12, soit environ 33,3%, car il y a 12 figures dans un jeu.
Formule du théorème de Bayes
P(A∣B)=P(B)P(A⋂B)=P(B)P(A)⋅P(B∣A)où :P(A)=La probabilité que A se produiseP(B )=La probabilité que B se produiseP(A∣B)=La probabilité que A soit donné BP(B∣A)=La probabilité que B soit donné AP(A⋂B))=La probabilité que A et B se produisent
Exemples de théorème de Bayes
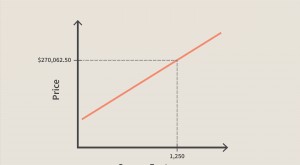
Vous trouverez ci-dessous deux exemples du théorème de Bayes dans lesquels le premier exemple montre comment la formule peut être dérivée dans un exemple d'investissement en actions à l'aide d'Amazon.com Inc. (AMZN). Le deuxième exemple applique le théorème de Bayes aux tests de médicaments pharmaceutiques.
Dérivation de la formule du théorème de Bayes
Le théorème de Bayes découle simplement des axiomes de probabilité conditionnelle. La probabilité conditionnelle est la probabilité d'un événement étant donné qu'un autre événement s'est produit. Par exemple, une simple question de probabilité peut demander :« Quelle est la probabilité que le cours de l'action Amazon.com baisse ? » La probabilité conditionnelle pousse cette question un peu plus loin en posant la question suivante :« Quelle est la probabilité que le cours de l'action AMZN baisse ? étant donné que l'indice Dow Jones Industrial Average (DJIA) a chuté plus tôt ?"
La probabilité conditionnelle de A étant donné que B s'est produit peut être exprimée comme :
Si A est :"Le prix AMZN baisse" alors P(AMZN) est la probabilité que AMZN baisse ; et B est :"DJIA est déjà en panne, " et P(DJIA) est la probabilité que le DJIA baisse ; alors l'expression de probabilité conditionnelle se lit comme « la probabilité que AMZN baisse compte tenu d'une baisse DJIA est égale à la probabilité que le prix AMZN baisse et que DJIA baisse sur la probabilité d'une baisse de l'indice DJIA.
P(AMZN|DJIA) =P(AMZN et DJIA) / P(DJIA)
P(AMZN et DJIA) est la probabilité de les deux A et B se produisent. C'est également la même chose que la probabilité que A se produise multipliée par la probabilité que B se produise étant donné que A se produit, exprimé comme P(AMZN) x P(DJIA|AMZN). Le fait que ces deux expressions soient égales conduit au théorème de Bayes, qui s'écrit :
si, P(AMZN et DJIA) =P(AMZN) x P(DJIA|AMZN) =P(DJIA) x P(AMZN|DJIA)
alors, P(AMZN|DJIA) =[P(AMZN) x P(DJIA|AMZN)] / P(DJIA).
Où P(AMZN) et P(DJIA) sont les probabilités de chute d'Amazon et du Dow Jones, sans égard les uns aux autres.
La formule explique la relation entre la probabilité de l'hypothèse avant de voir la preuve que P(AMZN), et la probabilité de l'hypothèse après avoir obtenu la preuve P(AMZN|DJIA), étant donné une hypothèse pour Amazon étant donné la preuve dans le Dow Jones.
Exemple numérique du théorème de Bayes
A titre d'exemple numérique, imaginez qu'il existe un test de dépistage de drogue précis à 98 %, ce qui signifie 98% du temps, il montre un vrai résultat positif pour quelqu'un qui utilise la drogue et 98% du temps il montre un vrai résultat négatif pour les non-utilisateurs de la drogue. Prochain, supposer que 0,5% des personnes utilisent le médicament. Si une personne choisie au hasard est positive au médicament, le calcul suivant peut être effectué pour voir si la probabilité que la personne soit réellement un utilisateur de la drogue.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 - 0,98) x (1 - 0,005))] =0,0049 / (0,0049 + 0,0199) =19,76 %
Le théorème de Bayes montre que même si une personne est positive dans ce scénario, il est en fait beaucoup plus probable que la personne ne consomme pas de drogue.
la finance
- Définition de la prise en charge de la dette
- Définition d'un codemandeur
- Définition de la moyenne géométrique
- Définition de l'évaluation
- Définition et explication de la garantie
- Une définition des temps d'intérêt gagnés
- Liquidité - Définition &Ratios
- Définition et explication des décaissements
- Fiduciaire - Définition &Responsabilité
-
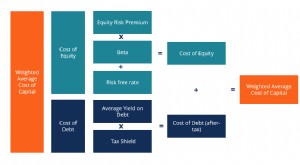 Définition du WACC
Définition du WACC Le coût moyen pondéré du capital (WACC) dune entreprise représente son coût combiné du capital. Coût du capital Le coût du capital est le taux de rendement minimum quune entreprise doit gagner avant d...
-
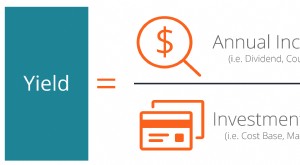 Qu'est-ce que le rendement (définition) ?
Qu'est-ce que le rendement (définition) ? Le rendement est défini comme un revenu sur investissement uniquement (il exclut les gains en capital. Rendement des gains en capital Le rendement des gains en capital (CGY) est lappréciation du prix ...