Un regard sur la méthode des options de Monte Carlo
Les Options de Monte-Carlo La méthode est un moyen d'analyser des investissements hautement volatils ou complexes en exécutant des modèles de divers résultats potentiels. La méthode utilise des entrées de différents facteurs qui peuvent affecter le profit d'un investissement hautement imprévisible. L'investissement est si imprévisible qu'aucun autre moyen d'évaluation ne pourrait mesurer correctement son rendement probable. Avec la méthode Monte Carlo, le rendement potentiel de l'option est considéré comme la moyenne de tous les différents résultats.
Histoire de la méthode Monte Carlo
La méthode a été introduite pour la première fois en 1964 lorsque les économistes ont noté qu'il y avait certains investissements avec lesquels l'analyse des risques traditionnelle ne pouvait pas être appliquée. Ces investissements sont soumis à un si large éventail de facteurs, aucun facteur ou groupe de facteurs ne pourrait être utilisé pour générer une mesure cohérente du risque et de la récompense. La meilleure façon de mesurer cela, alors, était de simuler différents scénarios susceptibles de se produire. C'est ce qu'on appelle la méthode "Monte Carlo" car elle utilise des modèles de probabilité utilisés dans le jeu pour estimer le risque et le rendement. Les investissements sont si variables qu'ils ressemblent beaucoup au jeu, la méthode semble donc appropriée pour certaines options et dérivés.
Application pratique de la méthode Monte Carlo
Cette méthode est souvent considérée comme un moyen de dernier recours. Elle s'applique uniquement dans les scénarios où d'autres, des mesures plus cohérentes du risque et du rendement ne sont pas possibles. Le Monte Carlo utilise une moyenne pour décrire le résultat d'une grande série de calculs dans lesquels le résultat moyen ne sera probablement pas atteint. Par exemple, la méthode de Monte Carlo pourrait être appliquée au lancer d'un jeu de dés. Les différents résultats seraient moyennés, et le résultat moyen serait d'obtenir un « 10 ». Bien qu'il s'agisse de la moyenne de tous les résultats possibles de lancer deux dés, il n'y a pas de probabilité plus élevée qu'un 10 sera obtenu que diverses autres combinaisons.
Quand utiliser la méthode Monte Carlo
Parce que la méthode n'est utilisée qu'en dernier recours, il est appliqué aux valeurs aberrantes du marché qui ne peuvent pas être estimées avec d'autres modèles. Il existe certains scénarios où la méthode Monte Carlo doit être appliquée de manière cohérente. Par exemple, il est souvent utilisé pour calculer le risque et la récompense des options asiatiques. Les options asiatiques sont en fait un endroit judicieux pour utiliser la méthode de Monte Carlo, car elles utilisent le prix sous-jacent moyen sur une période de temps définie pour déterminer le gain. Par conséquent, les moyennes utilisées dans la méthode de Monte Carlo fonctionnent bien pour mesurer leur rendement probable.
Quand éviter la méthode Monte Carlo
Si votre investissement pouvait être analysé de manière appropriée à l'aide d'une autre méthode de tarification et de récompenses, alors la méthode de Monte Carlo doit être évitée. La plupart des contrats d'options peuvent être analysés avec des chiffres tels que l'asymétrie de volatilité, et la méthode de Monte Carlo serait moins susceptible d'estimer un rendement réel que cette échelle. En outre, la méthode Monte Carlo prend beaucoup de temps pour générer une réponse. Étant donné que tant de simulations doivent être exécutées, elle est moins susceptible d'aboutir rapidement à une décision qu'une autre méthode d'analyse.
Options
-
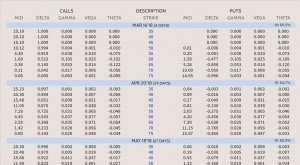 Utiliser les Grecs pour comprendre les options
Utiliser les Grecs pour comprendre les options Essayer de prédire ce quil adviendra du prix dune seule option ou dune position impliquant plusieurs options au fur et à mesure que le marché change peut être une entreprise difficile. Étant donné que...
-
 Qu'est-ce que la méthode de capitalisation directe ?
Qu'est-ce que la méthode de capitalisation directe ? La méthode de capitalisation directe sobtient en prenant les revenus enregistrés dans le temps et en les divisant par les taux de capitalisation respectifs retenus sur la même période. Le taux de capi...


