Quel est le taux d'intérêt annuel effectif ?

Le taux d'intérêt annuel effectif (TEAR) est le taux d'intérêt qui est ajusté pour la compositionTaux de croissance composéLe taux de croissance composé est une mesure utilisée spécifiquement dans les contextes d'affaires et d'investissement, qui indique le taux de croissance sur plusieurs périodes. C'est une mesure de la croissance constante d'une série de données. Le plus grand avantage du taux de croissance composé est que la métrique prend en considération l'effet composé. sur une période donnée. Tout simplement, le taux d'intérêt annuel effectif est le taux d'intérêtFrais d'intérêtsLes frais d'intérêts proviennent d'une entreprise qui se finance au moyen de dettes ou de contrats de location-acquisition. Les intérêts se trouvent dans le compte de résultat, mais peut aussi qu'un investisseur puisse gagner (ou payer) en un an après avoir pris en considération la composition.

L'EAR peut être utilisé pour évaluer les intérêts payables sur un prêt ou toute dette ou pour évaluer les revenus d'un investissement, comme un certificat de placement garanti (CPG) ou un compte d'épargne.

Le taux d'intérêt annuel effectif est également appelé taux d'intérêt effectif (TIE), taux équivalent annuel (TEA), ou taux effectif. Comparez-le au taux de pourcentage annuel (TAEG)Taux de pourcentage annuel (TAEG)Le taux de pourcentage annuel (TAEG) est le taux d'intérêt annuel qu'un individu doit payer sur un prêt, ou qu'ils reçoivent sur un compte de dépôt. Finalement, APR est un terme de pourcentage simple utilisé pour exprimer le montant numérique payé par un individu ou une entité chaque année pour le privilège d'emprunter de l'argent. qui est basé sur l'intérêt simpleIntérêt simpleFormule d'intérêt simple, définition et exemple. L'intérêt simple est un calcul d'intérêt qui ne tient pas compte de l'effet de la composition. Dans de nombreux cas, intérêts composés avec chaque période désignée d'un prêt, mais en cas d'intérêt simple, ce ne est pas. Le calcul de l'intérêt simple est égal au montant en principal multiplié par le taux d'intérêt, multiplié par le nombre de périodes..

La formule EAR est donnée ci-dessous :

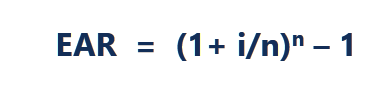
Où:

• je =Taux d'intérêt annuel déclaré
• m =Nombre de périodes de composition

Taux annuel effectif basé sur la composition

Le tableau ci-dessous montre la différence du taux annuel effectif lorsque les périodes de composition changent.

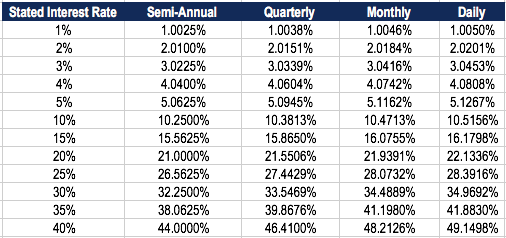
Tableau :Cours de base sur les titres à revenu fixe de CFI

Par exemple, le BAE d'un taux d'intérêt déclaré de 1 % composé trimestriellement est de 1,0038%.

Importance du taux annuel effectif

Le taux d'intérêt effectif annuel est un outil important qui permet d'évaluer le véritable retour sur investissement ou le véritable taux d'intérêt d'un prêt.

Le taux d'intérêt annuel indiqué et le taux d'intérêt effectif peuvent être sensiblement différents, en raison de la composition. Le taux d'intérêt effectif est important pour déterminer le meilleur prêt ou pour déterminer quel investissement offre le taux de rendement le plus élevé.Taux de rendement interne (TRI)Le taux de rendement interne (TRI) est le taux d'actualisation qui fait la valeur actuelle nette (VAN ) d'un projet zéro. En d'autres termes, il s'agit du taux de rendement annuel composé attendu qui sera obtenu sur un projet ou un investissement.

Dans le cas de la composition, l'EAR est toujours supérieur au taux d'intérêt annuel indiqué.

Exemple d'EAR

Par exemple, supposons que la banque offre votre dépôt de 10 $, 000 un taux d'intérêt déclaré de 12% composé mensuellement. Le tableau ci-dessous illustre la notion de taux d'intérêt annuel effectif :

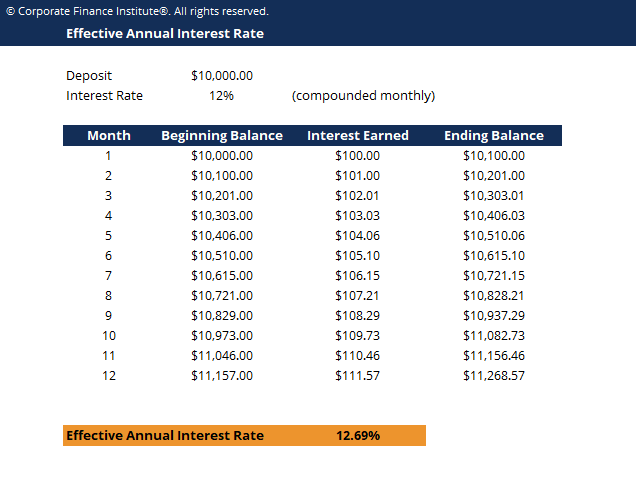Tableau :Cours de base sur les titres à revenu fixe de CFI

Intérêt du mois 1 :Solde d'ouverture (10 $, 000) x taux d'intérêt (12 %/12 =1 %) =100 $

Intérêt du mois 2 :Solde d'ouverture (10 $, 100) x taux d'intérêt (12 %/12 =1 %) =101 $

Le changement, en pourcentage, à partir du solde d'ouverture (10 $, 000) au solde de clôture (11 $, 268) est (11 $, 268 – 10 $, 000)/10$, 000 =0,12683 ou 12,683%, qui est le taux d'intérêt annuel effectif. Même si la banque offrait un taux d'intérêt déclaré de 12 %, votre argent a augmenté de 12,683% en raison de la composition mensuelle.

Le taux d'intérêt annuel effectif vous permet de déterminer le véritable retour sur investissement (ROI) Formule ROI (Return on Investment) Le retour sur investissement (ROI) est un ratio financier utilisé pour calculer l'avantage qu'un investisseur recevra par rapport à son coût d'investissement. Il est le plus souvent mesuré comme le revenu net divisé par le coût en capital initial de l'investissement. Plus le rapport est élevé, plus l'avantage gagné est grand..

Téléchargez le modèle gratuit

Entrez votre nom et votre e-mail dans le formulaire ci-dessous et téléchargez le modèle gratuit ci-dessus maintenant !

Comment calculer le taux d'intérêt effectif ?

Pour calculer le taux d'intérêt effectif à l'aide de la formule EAR, Suivez ces étapes:

1. Déterminer le taux d'intérêt indiqué

Le taux d'intérêt indiqué (également appelé taux annuel en pourcentage ou taux nominal) se trouve généralement dans les titres de l'accord de prêt ou de dépôt. Exemple :« Taux annuel 36 %, intérêts facturés mensuellement.

2. Déterminer le nombre de périodes de composition

Les périodes de composition sont généralement mensuelles ou trimestrielles. Les périodes de composition peuvent être de 12 (12 mois dans un an) et de 4 pour les trimestres (4 trimestres dans un an).

Pour votre référence :

• Mensuel =12 périodes de composition
• Trimestriel =4 périodes de composition
• Bi-hebdomadaire =26 périodes de composition
• Hebdomadaire =52 périodes de composition
• Quotidien =365 périodes de composition

3. Appliquer la formule EAR :EAR =(1+ i/n) ^m - 1

Où:

• • je =Taux d'intérêt déclaré
  • m =Périodes composées

Exemple

Pour calculer le taux d'intérêt annuel effectif d'une carte de crédit avec un taux annuel de 36 % et des intérêts facturés mensuellement :

1. Taux d'intérêt déclaré :36 %

2. Nombre de périodes de composition :12

Par conséquent, EAR =(1+0,36/12)^12 – 1 =0,4257 ou 42,57 %.

Pourquoi les banques n'utilisent-elles pas le taux d'intérêt annuel effectif ?

Lorsque les banques facturent des intérêts, le taux d'intérêt indiqué est utilisé à la place du taux d'intérêt annuel effectif. Ceci est fait pour faire croire aux consommateurs qu'ils paient un taux d'intérêt inférieur.

Par exemple, pour un prêt à un taux d'intérêt déclaré de 30%, composé mensuellement, le taux d'intérêt annuel effectif serait de 34,48 %. Les banques annoncent généralement le taux d'intérêt déclaré de 30 % plutôt que le taux d'intérêt effectif de 34,48 %.

Lorsque les banques paient des intérêts sur votre compte de dépôt, l'EAR est annoncé comme étant plus attrayant que le taux d'intérêt indiqué.

Par exemple, pour un dépôt à un taux déclaré de 10 % composé mensuellement, le taux d'intérêt annuel effectif serait de 10,47 %. Les banques annonceront le taux d'intérêt annuel effectif de 10,47 % plutôt que le taux d'intérêt déclaré de 10 %.

Essentiellement, ils indiquent le taux qui semble le plus favorable.

Lecture connexe

CFI est un fournisseur mondial de cours de modélisation financière et de certification d'analyste financier. Inscrivez-vous aujourd'hui !. Pour continuer à développer votre carrière de professionnel de la finance, consultez les ressources CFI supplémentaires suivantes :

• Rendement attenduRendement attenduLe retour attendu sur un investissement est la valeur attendue de la distribution de probabilité des retours possibles qu'il peut fournir aux investisseurs. Le retour sur investissement est une variable inconnue qui a différentes valeurs associées à différentes probabilités.
• Points de basePoints de base (BPS)Les points de base (BPS) sont la mesure couramment utilisée pour évaluer les variations des taux d'intérêt. Un point de base correspond à 1 centième d'un pour cent.
• Rendement des gains en capital Rendement des gains en capital Le rendement des gains en capital (CGY) est l'appréciation du prix d'un investissement ou d'un titre exprimé en pourcentage. Étant donné que le calcul du rendement du gain en capital fait intervenir le prix du marché d'un titre au fil du temps, il peut être utilisé pour analyser la fluctuation du prix du marché d'un titre. Voir calcul et exemple
• Coût moyen pondéré du capital (WACC)WACCWACC est le coût moyen pondéré du capital d'une entreprise et représente son coût mixte du capital, y compris les capitaux propres et la dette.