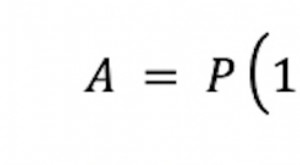Intérêt composé :formule et exemple

Il existe une légende urbaine selon laquelle Albert Einstein a appelé un jour l'intérêt composé « la force la plus puissante de l'univers ». Nous ne pouvons pas être sûrs qu'il l'a vraiment dit, mais le sentiment est certainement vrai :l'intérêt composé est un outil financier puissant pour accroître la richesse.

Mais alors qu'Einstein n'a eu aucun mal à comprendre l'intérêt composé, beaucoup de gens trouvent cela déroutant. Encore moins savent comment utiliser la formule des intérêts composés. Dans cet article, nous allons plonger profondément dans les intérêts composés. Il y a beaucoup de maths devant nous, mais nous allons vous guider lentement.

Wealthsimple Invest est un moyen automatisé de faire fructifier votre argent comme les investisseurs les plus avertis au monde. Commencez et nous vous construirons un portefeuille d'investissement personnalisé en quelques minutes.

Quelle est la formule des intérêts composés ?

L'intérêt composé est le principe selon lequel votre intérêt rapporte des intérêts. Puis cette l'intérêt rapporte l'intérêt. Et ça continue, encore et encore. Au fur et à mesure que votre solde augmente, vos paiements d'intérêts augmentent, ce qui à son tour augmente votre solde. Comme vous pouvez l'imaginer, les intérêts composés s'additionnent rapidement.

Si vous êtes familier avec l'intérêt simple, vous reconnaîtrez certaines des mêmes variables dans la formule des intérêts composés, mais avec quelques étapes supplémentaires. Voici la formule :

**Total principal et intérêts =P (1 + i)** m

Voici à quoi correspondent ces lettres :

• P =Principal du prêt (combien vous empruntez).

• i =Taux d'intérêt exprimé en pourcentage (par exemple pour un taux de 4%, utiliser 0.04.)

• n =Le nombre de périodes de composition. Ce sera différent pour chaque prêt. Certains composés annuellement, certains mensuels composés, etc. Vous trouverez ces informations avec les conditions de votre prêt.

Cette équation vous dira combien vous allez rembourser au total, y compris le principal d'origine. C'est un excellent moyen de le découvrir, par exemple, exactement combien cette voiture vous coûtera à long terme, ou le coût réel de vos prêts étudiants.

Si vous voulez savoir combien vous paierez d'intérêts, cependant, vous soustrayez simplement le principal d'origine à la fin de l'équation.

Intérêt seulement =[P (1 + i)n] - P

Cela vous indiquera le coût du prêt. C'est-à-dire, vous apprendrez exactement combien coûte le privilège d'emprunter de l'argent.

Comment utiliser la formule des intérêts composés

Maintenant que vous connaissez la formule, la prochaine étape est d'apprendre à l'utiliser.

Étape 1 :Résolvez les parenthèses

En raison de l'ordre des opérations (vous vous souvenez de celui du cours de mathématiques ?), nous résolvons le parenthèses d'une équation d'abord. Il n'y a qu'une seule parenthèse à résoudre dans ce cas et heureusement, c'est assez facile. Vous n'en ajoutez qu'un au taux d'intérêt. Si votre taux d'intérêt est de 2 %, alors la valeur entre parenthèses serait 1,02.

Étape 2 :Résoudre l'exposant

Après avoir résolu les parenthèses, vous résolvez ensuite les exposants. Dans le cas de la formule des intérêts composés, nous augmentons la valeur entre parenthèses au nombre de périodes de composition. S'il y a 12 périodes de composition, nous augmenterions notre 1,02 à la puissance 12 pour obtenir 1,27.

Étape 3 : Résoudre l'intérêt

Notre dernière étape consiste à multiplier ce que nous avons résolu par le principal d'origine du compte, investissement, ou prêt. Si vous avez initialement déposé 1 $, 000, nous multiplierions cela par 1,27 pour obtenir 1 $, 270. C'est le total que vous recevriez à la fin de la durée du prêt. Ensuite, vous pouvez soustraire le capital pour savoir ce que vous avez gagné en intérêts :1 $, 270.

Exemple de calcul des intérêts composés

Chaque fois que nous explorons des concepts mathématiques complexes, il est utile d'utiliser un exemple de la vie réelle pour nous aider à établir des relations. Passons en revue un exemple fictif d'intérêt composé.

Jean a 15 $, 000 il veut grandir. Sa banque propose des certificats de dépôt à 3 % composés mensuellement, mais son argent sera bloqué pendant quatre ans. S'il retire son argent plus tôt, il paiera une grosse amende. Il veut savoir combien d'argent il gagnera en intérêts.

Revenons à notre formule. Total principal et intérêts =P (1 + i)n

Si vous vous souvenez de notre formule, P est le principal, qui est le 15 $, 000 John veut déposer dans le CD. je est le taux d'intérêt, mais puisque nous n'utilisons pas 0.03. Les banques déclarent leur annuel taux d'intérêt, mais ce CD compose mensuellement, nous devons donc diviser 0,03 par 12 mois pour obtenir 0,0025. m est le nombre de périodes de composition, qui dans ce cas est de 36 (trois ans convertis en mois).

Voici donc notre équation : 15 $, 000 (1 + 0,0025)36=16 $, 410,77

C'est ce que John récupérera à la fin. Ce nombre comprend son investissement initial plus ses retours d'intérêts. Pour savoir combien d'intérêt il a gagné, nous déduisons simplement le principal initial de ce chiffre.

16 $, 410,77 - 15 $, 000 =1 $, 410,77

Pour vous aider à voir comment les intérêts composés s'additionnent au fil du temps, Regardons tous les paiements d'intérêts en un an du certificat de dépôt de John. Ce tableau vous indique le solde de départ au début du mois, combien d'intérêts ont été gagnés ce mois-là, et le solde de clôture du compte.

Mois Solde de départ Intérêts gagnés Solde de clôture 1$15, 000$37.50$15, 037.502$15, 037.50$37.59$15, 075.093$15, 075.09$37.69$15, 112.784$15, 112.78$37.78$15, 150.565$15, 150.56$37.87$15, 188.436$15, 188.43$37.98$15, 226.417$15, 226,41$38,07$15, 264.488$15, 264.48$38.16$15, 302.649$15, 302.64$38.25$15, 340.8910$15, 340.89$38.36$15, 379.2511$15, 379.25$38.45$15, 417.7012$15, 417.70$38.54$15, 456.24

Remarquez comment la colonne des intérêts gagnés augmente avec le temps. Il gagne plus d'argent par mois plus il détient le certificat de dépôt. La différence n'est pas énorme, mais c'est parce que John n'a investi que 15 $, 000. Imaginez si c'était son compte de retraite avec 200 $, 000 ou 300 $, 000 gagnant 8-12% sur 30 ans à travers un portefeuille diversifié de fonds négociés en bourse (ETF). L'intérêt s'additionne vite.

Pourquoi John se soucie-t-il du montant qu'il gagnera éventuellement en intérêts ? Parce que nous n'investissons pas dans le vide. Il existe d'innombrables opportunités d'investissement pour faire fructifier votre argent. Vous devez comprendre combien d'intérêts vous gagnerez sur un titre ou un produit d'investissement particulier, car vous pourrez ainsi identifier les investissements qui rapportent le plus.

Les avantages des intérêts composés

J'espère que vous comprenez maintenant comment utiliser la formule des intérêts composés. Mais cela soulève la question :pourquoi les intérêts composés sont-ils si importants ? Que peut-il faire pour nous ?

1. Votre argent fructifie plus rapidement avec le temps

Payer des intérêts composés est difficile car il peut sembler difficile de devancer la dette. Les cartes de crédit facturent des intérêts composés, c'est pourquoi de nombreuses personnes ont du mal à se sortir de la dette de carte de crédit. recevoir des intérêts composés, cependant, est merveilleux parce que votre argent augmente de plus en plus vite au fil du temps. Tout ce que vous avez à faire est de le laisser tranquille.

Lorsque vous placez de l'argent sur un compte d'épargne à haut rendement, les intérêts que vous recevez à chaque période sont ajoutés à votre solde. Votre nouveau solde est utilisé pour calculer le prochain paiement d'intérêts, qui comprend les intérêts que vous avez gagnés précédemment. Par conséquent, chaque paiement d'intérêt que vous recevez est légèrement plus important que le précédent (en supposant que vous ne retirez pas d'argent du compte).

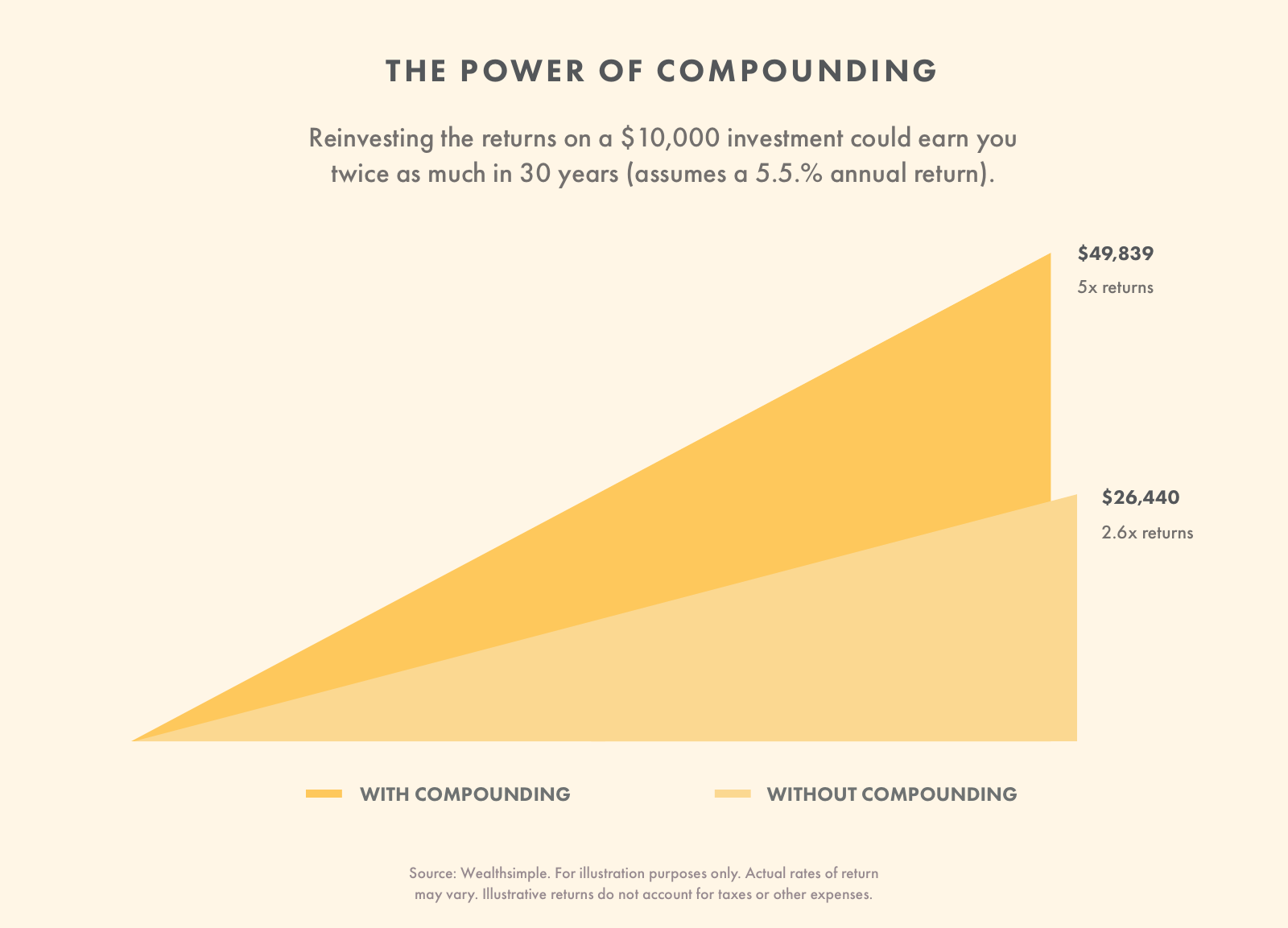
Par exemple, réinvestir les intérêts de 10 $, 000 pourraient gagner deux fois plus sur 30 ans que si vous deviez retirer les gains.

Cet effet boule de neige est un moyen puissant de créer de la richesse au fil du temps. C'est aussi pourquoi vous devriez résister à retirer de l'argent de vos comptes d'épargne et de placement.

Si vous utilisez un portefeuille d'investissement automatisé, il est préférable de cotiser régulièrement et de prétendre que l'argent n'existe pas avant la retraite. Chaque dollar que vous ajoutez à votre solde crée un peu plus d'intérêt, et chaque peu d'intérêt construit votre équilibre. Ce cycle est la façon dont les gens deviennent riches.

2. L'intérêt composé rapporte plus que l'intérêt simple

L'effet « intérêt d'intérêt » signifie qu'un investissement à intérêt composé rapportera toujours plus qu'un investissement à intérêt simple lorsque toutes les autres variables (principal, taux d'intérêt, et la durée) sont les mêmes.

Gardez ce mantra à l'esprit :il est préférable de Payer intérêt simple et recevoir intérêts composés.

3. L'intérêt composé est excitant et encourageant

Cela peut sembler idiot, mais voir l'intérêt croître dans un compte d'épargne ou un produit d'investissement est captivant :votre argent augmente sans avoir à contribuer de votre travail.

En réalité, le plaisir de voir l'argent fructifier encourage les gens à laisser leur argent dans leurs investissements et à contribuer davantage. Il est plus facile d'engager de l'argent dans un investissement si vous pouvez voir des croissance tangible chaque mois, surtout quand vous savez que chaque dollar que vous versez le fait croître plus rapidement.

4. Les intérêts composés vous aident à atteindre vos objectifs financiers

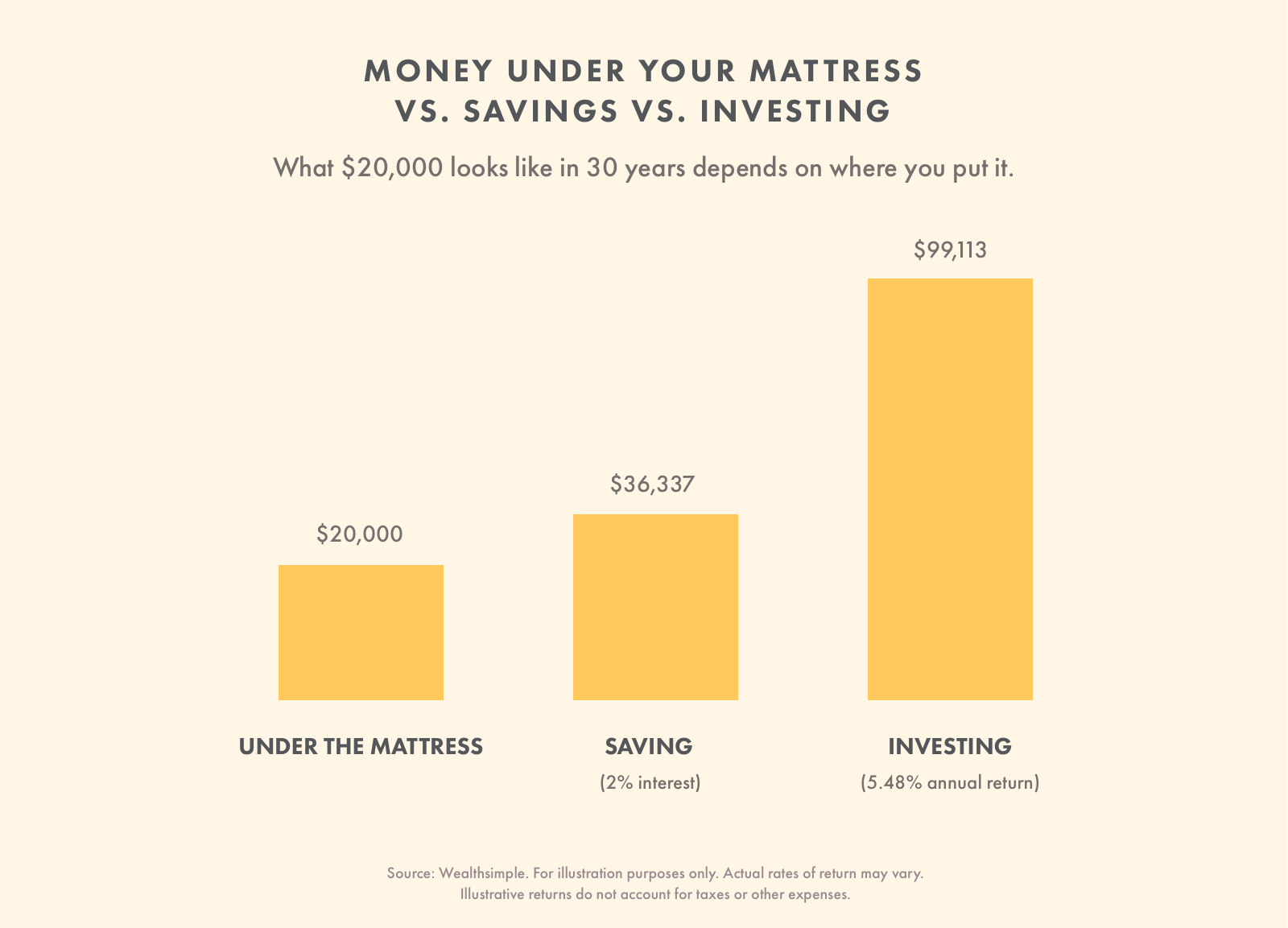
Le principal avantage des intérêts composés est qu'ils vous aident à atteindre vos objectifs financiers et à vous préparer à la retraite. Cacher de l'argent sous votre matelas est techniquement économiser pour l'avenir, mais il ne tient pas compte de la puissance d'un compte d'épargne à haut rendement ou d'un portefeuille d'investissement. Sans intérêt composé, vous auriez à travailler pour chaque dollar de votre pécule.

Et après

Appliquez votre nouvelle compréhension de la formule des intérêts composés chaque fois que vous envisagez un produit financier, investissement, ou prêt. Assurez-vous de bien comprendre le réel le coût ou l'avantage de votre argent avant de prendre votre décision.