Intérêts composés
Qu'est-ce que l'intérêt composé ?
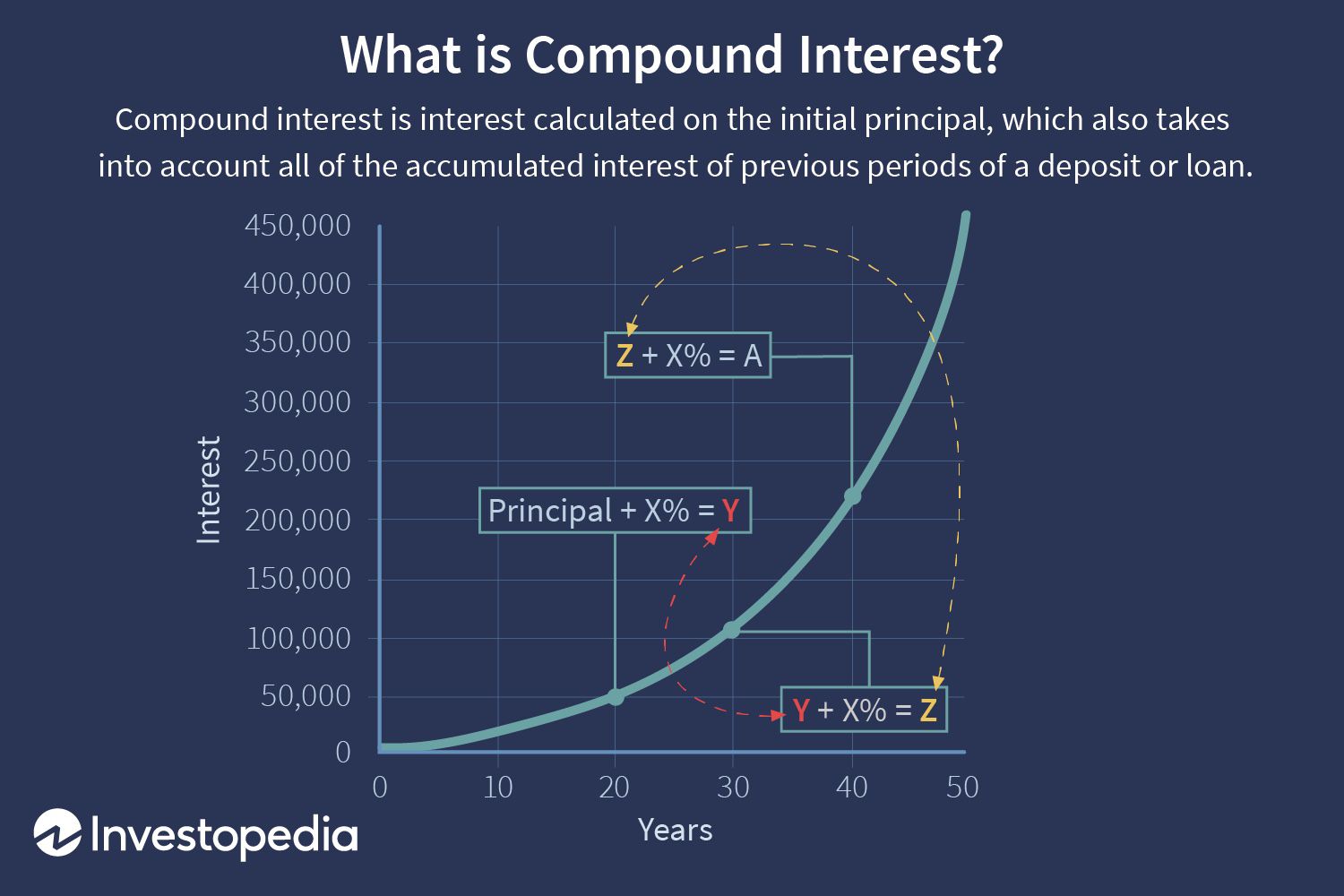
L'intérêt composé (ou intérêt composé) est l'intérêt sur un prêt ou un dépôt calculé sur la base à la fois du principal initial et des intérêts accumulés des périodes précédentes. Provenant de l'Italie du XVIIe siècle, les intérêts composés peuvent être considérés comme des « intérêts sur intérêts, " et fera croître une somme à un rythme plus rapide que le simple intérêt, qui est calculé uniquement sur le montant principal.
Le taux auquel les intérêts composés s'accumulent dépend de la fréquence de la composition, tel que plus le nombre de périodes de composition est élevé, plus l'intérêt composé est élevé. Ainsi, le montant des intérêts composés courus sur 100 $ composé à 10 % annuellement sera inférieur à celui sur 100 $ composé à 5 % semestriellement au cours de la même période. Étant donné que l'effet des intérêts sur intérêts peut générer des rendements de plus en plus positifs sur la base du montant initial du capital, la composition a parfois été appelée le "miracle de l'intérêt composé".
Points clés à retenir
- Les intérêts composés (ou intérêts composés) sont des intérêts calculés sur le capital initial, qui comprend également tous les intérêts accumulés des périodes précédentes sur un dépôt ou un prêt.
- L'intérêt composé est calculé en multipliant le montant du capital initial par un plus le taux d'intérêt annuel majoré du nombre de périodes composées moins un.
- L'intérêt peut être composé sur n'importe quel calendrier de fréquence donné, de continu à quotidien à annuel.
- Lors du calcul des intérêts composés, le nombre de périodes de composition fait une différence significative.
Comprendre les intérêts composés
Comment fonctionne l'intérêt composé
L'intérêt composé est calculé en multipliant le montant du capital initial par un plus le taux d'intérêt annuel majoré du nombre de périodes composées moins un. Le montant initial total du prêt est ensuite soustrait de la valeur résultante.
La formule de calcul du montant des intérêts composés est la suivante :
- Intérêts composés =montant total du principal et des intérêts futurs (ou valeur future) moins montant en principal actuel (ou valeur actuelle)
=[P (1 + je ) m ] – P
=P [(1 + je ) m - 1]
Où:
P =principal
je =taux d'intérêt annuel nominal en pourcentage
n =nombre de périodes de composition
Prenez un prêt de 10 $ sur trois ans, 000 à un taux d'intérêt de 5 % composé annuellement. Quel serait le montant des intérêts ? Dans ce cas, ce serait:
10 $, 000 [(1 + 0,05) 3 – 1] =10 $, 000 [1.157625 – 1] =$1, 576,25
Comment l'intérêt composé augmente
Étant donné que les intérêts composés comprennent les intérêts accumulés au cours des périodes précédentes, il grandit à un rythme toujours plus rapide. Dans l'exemple ci-dessus, bien que le total des intérêts payables sur la période de trois ans de ce prêt soit de 1 $, 576,25, le montant des intérêts n'est pas le même pour les trois années, comme ce serait avec un simple intérêt. Les intérêts payables à la fin de chaque année sont indiqués dans le tableau ci-dessous.
Les intérêts composés peuvent augmenter considérablement les rendements des investissements à long terme. Alors qu'un 100 $, 000 dépôt qui reçoit 5% d'intérêt annuel simple rapporterait 50 $, 000 d'intérêt total sur 10 ans, l'intérêt composé annuel de 5 % sur 10 $, 000 équivaudrait à 62 $, 889,46 sur la même période. Si la période de composition était plutôt payée mensuellement sur la même période de 10 ans à un taux d'intérêt composé de 5 %, l'intérêt total passerait plutôt à 64 $, 700,95.
Barèmes d'intérêts composés
L'intérêt peut être composé sur n'importe quel calendrier de fréquence donné, de quotidien à annuel. Il existe des calendriers de fréquence de composition standard qui sont généralement appliqués aux instruments financiers.
Le calendrier de composition couramment utilisé pour les comptes d'épargne dans les banques est quotidien. Pour un CD, les programmes de fréquence de composition typiques sont quotidiens, mensuel, ou semestriellement ; pour les comptes du marché monétaire, c'est souvent quotidien. Pour les crédits immobiliers, prêts sur valeur domiciliaire, prêts commerciaux personnels, ou des comptes de carte de crédit, le calendrier de composition le plus couramment appliqué est mensuel.
Il peut également y avoir des variations dans le délai dans lequel les intérêts courus sont réellement crédités sur le solde existant. Les intérêts sur un compte peuvent être composés quotidiennement mais uniquement crédités mensuellement. Ce n'est que lorsque les intérêts sont effectivement crédités, ou ajouté au solde existant, qu'il commence à gagner des intérêts supplémentaires sur le compte.
Certaines banques offrent également ce qu'on appelle des intérêts composés en continu, ce qui ajoute de l'intérêt au capital à chaque instant possible. A des fins pratiques, il ne s'accumule pas beaucoup plus que les intérêts composés quotidiens, à moins que vous ne vouliez y mettre de l'argent et le retirer le même jour.
Une composition plus fréquente des intérêts est avantageuse pour l'investisseur ou le créancier. Pour un emprunteur, le contraire est vrai.
Périodes de composition
Lors du calcul des intérêts composés, le nombre de périodes de composition fait une différence significative. La règle de base est que plus le nombre de périodes de composition est élevé, plus le montant des intérêts composés est élevé.
Le tableau suivant montre la différence que le nombre de périodes de composition peut faire pour 10 $, 000 prêt avec un taux d'intérêt annuel de 10 % sur une période de 10 ans.
Considérations particulières
L'intérêt composé est étroitement lié à la valeur temps de l'argent et à la règle de 72, deux concepts importants dans l'investissement.
Valeur temporelle de l'argent
Comprendre la valeur temporelle de l'argent et la croissance exponentielle créée par la capitalisation est essentiel pour les investisseurs qui cherchent à optimiser leur allocation de revenu et de patrimoine.
La formule pour obtenir la valeur future (FV) et la valeur actuelle (PV) sont les suivantes :
FV =PV (1 +i) m et PV =FV / (1 + i) m
Par exemple, la valeur future de 10 $, 000 composé à 5 % par an pendant trois ans :
=10 $, 000 (1 + 0,05) 3
=10 $, 000 (1.157625)
=11 $, 576,25
La valeur actuelle de 11 $, 576,25 actualisé à 5% pendant trois ans :
=11 $, 576,25 / (1 + 0,05) 3
=11 $, 576,25 / 1,157625
=10 $, 000
La réciproque de 1.157625, qui est égal à 0,8638376, est le facteur d'actualisation dans ce cas.
Règle de 72 Considération
La règle dite de 72 calcule le temps approximatif sur lequel un investissement doublera à un taux de rendement ou d'intérêt donné "i, " et est donné par (72/i). Il ne peut être utilisé que pour la composition annuelle.
Par exemple, un investissement qui a un taux de rendement annuel de 6 % doublera en 12 ans. Un investissement avec un taux de rendement annuel de 8 % doublera ainsi en neuf ans.
Taux de croissance annuel composé (TCAC)
Le taux de croissance annuel composé (TCAC) est utilisé pour la plupart des applications financières qui nécessitent le calcul d'un taux de croissance unique sur une période de temps.
Disons que votre portefeuille de placements est passé de 10 $, 000 à 16 $, 000 sur cinq ans; qu'est-ce que le TCAC ? Essentiellement, cela signifie que PV =-10$, 000, VF =16 $, 000, et nt =5, donc la variable "i" doit être calculée. À l'aide d'une calculatrice financière ou d'Excel, on peut montrer que i =9,86 %.
Selon la convention de trésorerie, votre investissement initial (PV) de 10 $, 000 est affiché avec un signe négatif car il représente une sortie de fonds. PV et FV doivent nécessairement avoir des signes opposés pour résoudre "i" dans l'équation ci-dessus.
Applications réelles du TCAC
Le TCAC est largement utilisé pour calculer les rendements sur des périodes de temps pour les actions, fonds communs de placement, et les portefeuilles d'investissement. Le TCAC est également utilisé pour déterminer si un gestionnaire de fonds communs de placement ou un gestionnaire de portefeuille a dépassé le taux de rendement du marché sur une période de temps. Si, par exemple, un indice boursier a fourni des rendements totaux de 10 % sur une période de cinq ans, mais un gestionnaire de fonds n'a généré que des rendements annuels de 9% sur la même période, le gestionnaire a sous-performé le marché.
Le TCAC peut également être utilisé pour calculer le taux de croissance attendu des portefeuilles d'investissement sur de longues périodes, ce qui est utile à des fins telles que l'épargne pour la retraite. Considérez les exemples suivants :
Exemple 1: Un investisseur averse au risque est satisfait d'un modeste taux de rendement annuel de 3 % sur son portefeuille. Son cadeau de 100$, 000 portefeuille serait, donc, passer à 180 $, 611 après 20 ans. En revanche, un investisseur tolérant au risque qui s'attend à un rendement annuel de 6 % sur son portefeuille verrait 100 $, 000 passer à 320 $, 714 après 20 ans.
Exemple 2 : Le TCAC peut être utilisé pour estimer combien doit être stocké pour économiser pour un objectif spécifique. Un couple qui aimerait économiser 50 $, 000 sur 10 ans pour une mise de fonds sur un condo devrait économiser 4 $, 165 par an s'ils assument un rendement annuel (TCAC) de 4 % sur leur épargne. S'ils sont prêts à prendre un peu plus de risques et à s'attendre à un TCAC de 5 %, ils devraient économiser 3 $, 975 par an.
Exemple 3 : Le TCAC peut également démontrer les vertus d'investir plus tôt que tard dans la vie. Si l'objectif est d'économiser 1 million de dollars à la retraite à 65 ans, sur la base d'un TCAC de 6 %, un jeune de 25 ans devrait économiser 6 $, 462 par an pour atteindre cet objectif. Une personne de 40 ans, d'autre part, il faudrait économiser 18 $, 227, ou presque trois fois ce montant, pour atteindre le même but.
- Les TCAC apparaissent également fréquemment dans les données économiques. Voici un exemple :le PIB par habitant de la Chine est passé de 193 $ en 1980 à 6 $, 091 en 2012. Quelle est la croissance annuelle du PIB par habitant sur cette période de 32 ans ? Le taux de croissance « i » dans ce cas s'avère être un impressionnant 11,4 %.
Avantages et inconvénients de la composition
Bien que le miracle de la composition ait conduit à l'histoire apocryphe d'Albert Einstein l'appelant la huitième merveille du monde ou la plus grande invention de l'homme, la capitalisation peut également jouer contre les consommateurs qui ont des prêts qui portent des taux d'intérêt très élevés, comme la dette de carte de crédit. Un solde de carte de crédit de 20 $, 000 portés à un taux d'intérêt de 20 % composé mensuellement donneraient un intérêt composé total de 4 $, 388 sur un an ou environ 365 $ par mois.
Du côté positif, la capitalisation peut fonctionner à votre avantage en ce qui concerne vos investissements et peut être un puissant facteur de création de richesse. La croissance exponentielle des intérêts composés est également importante pour atténuer les facteurs d'érosion de la richesse, comme l'augmentation du coût de la vie, inflation, et un pouvoir d'achat réduit.
Les fonds communs de placement offrent aux investisseurs l'un des moyens les plus simples de profiter des avantages des intérêts composés. Le choix de réinvestir les dividendes provenant du fonds commun de placement entraîne l'achat d'un plus grand nombre d'actions du fonds. Plus d'intérêts composés s'accumulent au fil du temps, et le cycle d'achat d'actions supplémentaires continuera d'aider l'investissement dans le fonds à prendre de la valeur.
Considérez un placement dans un fonds commun de placement ouvert avec un montant initial de 5 $, 000 et un ajout annuel de 2 $, 400. Avec un rendement annuel moyen de 12 % sur 30 ans, la valeur future du fonds est de 798 $, 500. L'intérêt composé est la différence entre les liquidités apportées à un investissement et la valeur future réelle de l'investissement. Dans ce cas, en versant 77 $, 000, ou une contribution cumulative de seulement 200 $ par mois, plus de 30 ans, l'intérêt composé est de 721 $ 500 du futur solde.
Bien sûr, les revenus d'intérêts composés sont imposables, à moins que l'argent ne soit dans un compte à l'abri de l'impôt ; il est normalement imposé au taux standard associé à la tranche d'imposition du contribuable.
Placements à intérêt composé
Un investisseur qui opte pour un plan de réinvestissement dans un compte de courtage utilise essentiellement le pouvoir de capitaliser tout ce qu'il investit.
Les investisseurs peuvent également subir des intérêts composés avec l'achat d'une obligation à coupon zéro. Les émissions obligataires traditionnelles offrent aux investisseurs des paiements d'intérêts périodiques basés sur les conditions initiales de l'émission obligataire, et parce que ceux-ci sont versés à l'investisseur sous forme de chèque, l'intérêt ne se compose pas. Les obligations à coupon zéro n'envoient pas de chèques d'intérêts aux investisseurs; au lieu, ce type d'obligation est acheté à un prix inférieur à sa valeur d'origine et croît avec le temps. Les émetteurs d'obligations à coupon zéro utilisent le pouvoir de la capitalisation pour augmenter la valeur de l'obligation afin qu'elle atteigne son plein prix à l'échéance.
Le compoundage peut également fonctionner pour vous lors des remboursements de prêts. Effectuer la moitié de votre versement hypothécaire deux fois par mois, par exemple, plutôt que d'effectuer le paiement intégral une fois par mois, finira par réduire votre période d'amortissement et vous faire économiser un montant substantiel d'intérêts.
Comment calculer l'intérêt composé
Si ça fait longtemps que tu n'as pas été en cours de maths, n'ayez crainte :il existe des outils pratiques pour déterminer la composition. De nombreuses calculatrices (à la fois portables et informatiques) ont des fonctions d'exposant que vous pouvez utiliser à ces fins.
Calcul des intérêts composés dans Excel
Si des tâches de composition plus compliquées surviennent, vous pouvez les exécuter dans Microsoft Excel—de trois manières différentes.
- La première façon de calculer les intérêts composés est de multiplier le nouveau solde de chaque année par le taux d'intérêt. Supposons que vous déposez 1 $, 000 sur un compte d'épargne avec un taux d'intérêt de 5 % composé annuellement, et vous voulez calculer le solde dans cinq ans. Dans Microsoft Excel, entrez « Année » dans la cellule A1 et « Solde » dans la cellule B1. Entrez les années 0 à 5 dans les cellules A2 à A7. Le solde pour l'année 0 est de 1 $, 000, vous devez donc entrer "1000" dans la cellule B2. Prochain, entrez "=B2*1.05" dans la cellule B3. Ensuite, entrez "=B3*1.05" dans la cellule B4 et continuez jusqu'à ce que vous arriviez à la cellule B7. Dans la cellule B7, le calcul est "=B6*1.05". Finalement, la valeur calculée dans la cellule B7—$1, 276,28—est le solde de votre compte d'épargne après cinq ans. Pour trouver la valeur des intérêts composés, soustraire $1, 000 à partir de 1 $, 276,28 ; cela vous donne une valeur de 276,28 $.
- La deuxième façon de calculer les intérêts composés consiste à utiliser une formule fixe. La formule des intérêts composés est ((P*(1+i)^n) - P), où P est le principal, i est le taux d'intérêt annuel, et n est le nombre de périodes. En utilisant les mêmes informations ci-dessus, entrez "Valeur principale" dans la cellule A1 et 1000 dans la cellule B1. Prochain, entrez "Taux d'intérêt" dans la cellule A2 et ".05" dans la cellule B2. Entrez « Périodes composées » dans la cellule A3 et « 5 » dans la cellule B3. Vous pouvez maintenant calculer l'intérêt composé dans la cellule B4 en entrant "=(B1*(1+B2)^B3)-B1", ce qui vous donne 276,28 $.
- Une troisième façon de calculer les intérêts composés consiste à créer une fonction macro. Démarrez d'abord Visual Basic Editor, qui se trouve dans l'onglet développeur. Cliquez sur le menu Insertion, et cliquez sur Module. Tapez ensuite "Function Compound_Interest (P As Double, Je comme double, N As Double) As Double" dans la première ligne. Sur la deuxième ligne, appuyez sur la touche de tabulation et tapez "Compound_Interest =(P*(1+i)^n) - P." Sur la troisième ligne du module, entrez "Fin de fonction". Vous avez créé une macro de fonction pour calculer le taux d'intérêt composé. En continuant à partir de la même feuille de calcul Excel ci-dessus, entrez "Intérêt composé" dans la cellule A6 et entrez "=Compound_Interest (B1, B2, B3)." Cela vous donne une valeur de 276,28 $, ce qui est cohérent avec les deux premières valeurs.
Autres calculateurs d'intérêts composés
Un certain nombre de calculateurs d'intérêts composés gratuits sont offerts en ligne, et de nombreuses calculatrices portables peuvent également effectuer ces tâches.
- Le calculateur d'intérêt composé gratuit offert par Financial-Calculators.com est simple à utiliser et propose des choix de fréquence composés de tous les jours à tous les ans. Il comprend une option pour sélectionner la composition continue et permet également la saisie des dates de début et de fin du calendrier réel. Après avoir saisi les données de calcul nécessaires, les résultats montrent les intérêts gagnés, valeur future, rendement annuel en pourcentage ou APY) (une mesure qui comprend la composition), et l'intérêt quotidien.
- Investor.gov, un site Web exploité par la Securities and Exchange Commission (SEC) des États-Unis, propose un calculateur d'intérêt composé en ligne gratuit. La calculatrice est assez simple, mais il permet des entrées de dépôts supplémentaires mensuels au principal, ce qui est utile pour calculer les revenus lorsque des économies mensuelles supplémentaires sont déposées.
- Un calculateur d'intérêts en ligne gratuit avec quelques fonctionnalités supplémentaires est disponible sur TheCalculatorSite.com. Cette calculatrice permet des calculs pour différentes devises, la possibilité de prendre en compte les dépôts ou retraits mensuels, et la possibilité de faire calculer automatiquement les augmentations ajustées en fonction de l'inflation des dépôts ou des retraits mensuels.
Comment puis-je savoir si les intérêts sont composés ?
La Truth in Lending Act (TILA) exige que les prêteurs divulguent les conditions du prêt aux emprunteurs potentiels, y compris le montant total des intérêts à rembourser sur la durée du prêt et si les intérêts courent simplement ou sont composés.
Une autre méthode consiste à comparer le taux d'intérêt d'un prêt à son taux annuel en pourcentage (TAEG), que la TILA exige également que les prêteurs divulguent. Le TAEG convertit les charges financières de votre prêt, qui comprennent tous les intérêts et frais, à un taux d'intérêt simple. Une différence substantielle entre le taux d'intérêt et le TAEG signifie l'un ou les deux scénarios :votre prêt utilise des intérêts composés, ou il comprend des frais de prêt élevés en plus des intérêts. Même lorsqu'il s'agit du même type de prêt, la gamme APR peut varier énormément entre les prêteurs en fonction des frais de l'institution financière et d'autres coûts.
Vous remarquerez que le taux d'intérêt qui vous est facturé dépend également de votre crédit. Les prêts offerts à ceux qui ont un excellent crédit portent des taux d'intérêt nettement inférieurs à ceux facturés aux emprunteurs dont le crédit est médiocre.
Qu'est-ce qu'une définition simple de l'intérêt composé ?
Les intérêts composés désignent le phénomène par lequel les intérêts associés à un compte bancaire, prêter, ou l'investissement augmente de manière exponentielle, plutôt que linéaire, au fil du temps. La clé pour comprendre le concept est le mot « composé ».
Supposons que vous investissiez 100 $ dans une entreprise qui vous verse un dividende de 10 % chaque année. Vous avez le choix d'empocher ces paiements de dividendes comme de l'argent liquide ou de réinvestir ces paiements dans des actions supplémentaires. Si vous choisissez la deuxième option, réinvestir les dividendes et les combiner avec votre investissement initial de 100 $, alors les retours que vous générez commenceront à croître avec le temps.
À qui profite l'intérêt composé ?
Tout simplement, les intérêts composés profitent aux investisseurs, mais le sens du mot « investisseurs » peut être assez large. Banques, par exemple, bénéficier d'intérêts composés lorsqu'ils prêtent de l'argent et réinvestir les intérêts qu'ils reçoivent dans l'octroi de prêts supplémentaires. Les déposants bénéficient également d'intérêts composés lorsqu'ils perçoivent des intérêts sur leurs comptes bancaires, obligations, ou d'autres investissements.
Il est important de noter que même si le terme « intérêts composés » comprend le mot « intérêts, ” le concept s'applique au-delà des situations pour lesquelles le mot intérêt est typiquement utilisé, tels que les comptes bancaires et les prêts.
Les intérêts composés peuvent-ils vous rendre riche ?
Oui. En réalité, les intérêts composés sont sans doute la force la plus puissante jamais conçue pour générer de la richesse. Il existe des registres de marchands, prêteurs, et divers hommes d'affaires utilisant des intérêts composés pour devenir riches pendant littéralement des milliers d'années. Dans l'ancienne ville de Babylone, par exemple, des tablettes d'argile ont été utilisées sur 4, il y a 000 ans pour enseigner aux élèves les mathématiques des intérêts composés.
Dans les temps modernes, Warren Buffett est devenu l'une des personnes les plus riches du monde grâce à une stratégie commerciale qui impliquait de composer avec diligence et patience ses retours sur investissement sur de longues périodes. Il est probable que, sous une forme ou une autre, les gens utiliseront les intérêts composés pour générer de la richesse dans un avenir prévisible.
Des économies
- Comment rembourser une dette rapidement
- Votre taux d'épargne :pourquoi et comment le calculer
- Salem Five Direct lève APY sur compte d'épargne,
- 3 façons de budgétiser une dépense ponctuelle
- Troisième contrôle de relance et plan de sauvetage COVID-19 :comment les 100 premiers jours de Biden pourraient avoir un impact sur votre argent
- Les comptes du club de Noël sont-ils toujours une bonne idée ?
-
 Comment empêcher les économies automatisées d'entraîner des frais de découvert
Comment empêcher les économies automatisées d'entraîner des frais de découvert Cela semble irrésistible :externalisez votre tâche bancaire vers une application afin que la tâche soit effectuée automatiquement. Et ces dernières années, cest une proposition que toutes sortes de ...
-
 Combien cela coûte-t-il d'expédier une voiture du Texas au New Jersey ?
Combien cela coûte-t-il d'expédier une voiture du Texas au New Jersey ? Lexpédition de base dune berline du Texas au New Jersey peut coûter aussi peu que 730 $. Il y en a 1, 810 milles entre San Antonio, Texas, et Newark, New Jersey - cest-à-dire du centre du Texas au ce...
-
 Avantages et inconvénients des services bancaires électroniques
Avantages et inconvénients des services bancaires électroniques Une fois une nouveauté, la banque électronique sur Internet est devenue aussi courante que les achats en ligne. Ce nest pas surprenant car il offre une commodité et une flexibilité quune succursale ba...
-
 Les avantages et les inconvénients de l'utilisation d'une carte Crypto Rewards
Les avantages et les inconvénients de l'utilisation d'une carte Crypto Rewards Beaucoup ou tous les produits ici proviennent de nos partenaires qui nous paient une commission. Cest comme ça quon gagne de largent. Mais notre intégrité éditoriale garantit que les opinions de nos e...



