Qu'est-ce que la durée de Macaulay ?
La duration de Macaulay est la moyenne pondérée du temps nécessaire pour recevoir les flux de trésorerie d'une obligation. Elle se mesure en unités d'années. La durée de Macaulay indique la durée moyenne pondérée pendant laquelle une obligation doit être détenue de sorte que la valeur actuelle totale des flux de trésorerie reçus soit égale au prix du marché actuel payé pour l'obligation. Il est souvent utilisé dans les stratégies d'immunisation obligataire.

Sommaire
- La duration de Macaulay mesure la moyenne pondérée du temps nécessaire pour recevoir les flux de trésorerie d'une obligation de sorte que la valeur actuelle des flux de trésorerie soit égale au prix de l'obligation.
- La durée de Macaulay d'une obligation est positivement liée à la durée jusqu'à l'échéance et inversement au taux d'intérêt nominal et au taux d'intérêt de l'obligation.
- La duration modifiée mesure la sensibilité du prix d'une obligation à la variation des taux d'intérêt.
Comment calculer la durée de Macaulay
Dans la durée de Macaulay, le temps est pondéré par le pourcentage de la valeur actuelle de chaque flux de trésorerie par rapport au prix du marché. valeur nominale, rendement et durée jusqu'à l'échéance. La tarification des obligations permet aux investisseurs d'une obligation. Par conséquent, il est calculé en additionnant tous les multiples des valeurs actuelles des flux de trésorerie et des périodes correspondantes, puis en divisant la somme par le prix des obligations du marché.
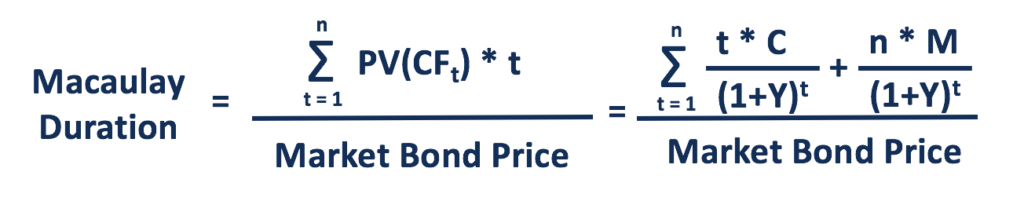
Où:
- PV(CF
t ) – Valeur actuelle des flux de trésorerie (coupon) à la période t - t – Période de temps pour chaque flux de trésorerie
- C – Paiement périodique des coupons
- m – Nombre total de périodes jusqu'à l'échéance
- M – Valeur à maturité
- Oui – Rendement périodique
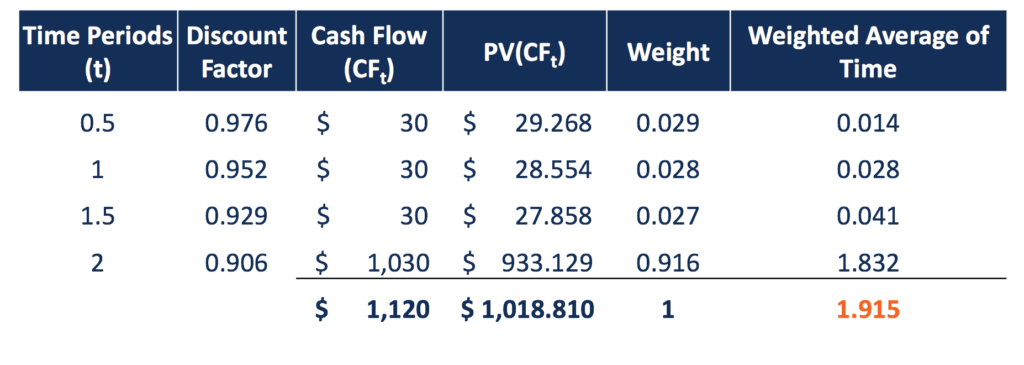
Par exemple, une obligation de 2 ans avec un 1 $, 000 par paie un coupon de 6 % semestriellement, et le taux d'intérêt annuel est de 5%. Ainsi, le prix du marché de l'obligation est de 1 $, 018.81, additionnant les valeurs actuelles de tous les flux de trésorerie. Le temps nécessaire pour recevoir chaque flux de trésorerie est ensuite pondéré par la valeur actuelle de ce flux de trésorerie par rapport au prix du marché.
La durée de Macaulay est la somme de ces périodes de temps moyennes pondérées, qui est de 1,915 ans. Un investisseur doit détenir l'obligation pendant 1,915 ans pour que la valeur actuelle des flux de trésorerie reçus compense exactement le prix payé.
Facteurs qui affectent la durée de Macaulay
La durée de Macaulay d'une obligation peut être affectée par le taux de coupon de l'obligationTaux de couponUn taux de coupon est le montant des revenus d'intérêts annuels payés à un détenteur d'obligations, sur la base de la valeur nominale de l'obligation., terme jusqu'à l'échéance, et rendement à l'échéanceRendement à l'échéance (YTM)Le rendement à l'échéance (YTM) - autrement appelé remboursement ou rendement comptable - est le taux de rendement spéculatif ou le taux d'intérêt d'un titre à taux fixe. Tous les autres facteurs étant constants, une obligation avec une échéance plus longue suppose une durée Macaulay plus longue, car il faut plus de temps pour recevoir le paiement du capital à l'échéance. Cela signifie également que la durée de Macaulay diminue avec le temps (la durée jusqu'à l'échéance diminue).
La durée de Macaulay est en relation inverse avec le taux du coupon. Plus les paiements de coupons sont élevés, plus la durée est faible, avec des montants en espèces plus importants payés dans les premières périodes. Une obligation à coupon zéro suppose la durée de Macaulay la plus élevée par rapport aux obligations à coupon, en supposant que les autres caractéristiques sont les mêmes. Elle est égale à l'échéance d'une obligation à coupon zéroObligation à coupon zéroUne obligation à coupon zéro est une obligation qui ne rapporte aucun intérêt et se négocie avec une décote par rapport à sa valeur nominale. On l'appelle également obligation à escompte pur ou obligation à escompte profond. et est inférieure à l'échéance des obligations à coupon.
La durée de Macaulay démontre également une relation inverse avec le rendement à l'échéance. Une obligation avec un rendement à l'échéance plus élevé affiche une duration Macaulay plus faible.
Durée de Macaulay par rapport à la durée modifiée
La durée modifiée est un autre type de durée fréquemment utilisé pour les obligations. Différent de la durée de Macaulay, qui mesure le temps moyen pour recevoir la valeur actuelle des flux de trésorerie équivalents au prix actuel de l'obligation, La durée modifiée identifie le sensibilité du prix de l'obligation à la variation du taux d'intérêt. Il est ainsi mesuré en pourcentage de variation du prix.
La durée modifiée peut être calculée en divisant la durée Macaulay de l'obligation par 1 plus le taux d'intérêt périodique, ce qui signifie que la duration modifiée d'une obligation est généralement inférieure à sa duration de Macaulay. Si une obligation est continuellement composée, la duration modifiée de l'obligation est égale à la duration de Macaulay.
Dans l'exemple ci-dessus, l'obligation présente une duration Macaulay de 1,915, et l'intérêt semestriel est de 2,5 %. Par conséquent, la Durée modifiée de l'obligation est 1,868 (1.915 / 1.025). Cela signifie pour chaque pourcentage d'augmentation (diminution) du taux d'intérêt, le prix de l'obligation baissera (augmentera) de 1,868%.
Une autre différence entre la durée de Macaulay et la durée modifiée est que la première ne peut être appliquée qu'aux instruments à revenu fixe qui généreront flux de trésorerie fixes . Pour les obligations dont les flux de trésorerie ou le calendrier des flux de trésorerie ne sont pas fixes, comme les obligations avec option d'achat ou de vente, la période elle-même et son poids sont incertains.
Par conséquent, à la recherche d'une durée de Macaulay, dans ce cas, n'a pas de sens. Cependant, La duration modifiée peut toujours être calculée puisqu'elle ne prend en compte que l'effet du changement de rendement, quelle que soit la structure des flux de trésorerie, qu'ils soient fixes ou non.
Durée de Macaulay et immunisation par lien
En gestion de portefeuille actif-passif, l'appariement de durée est une méthode d'immunisation des taux d'intérêt. Une variation du taux d'intérêt affecte la valeur actuelle des flux de trésorerie, et affecte ainsi la valeur d'un portefeuille de titres à revenu fixe. En faisant correspondre les durées entre les actifs et les passifs du portefeuille d'une entreprise, la variation du taux d'intérêt déplacera la valeur des actifs et la valeur des passifs exactement du même montant, mais dans des directions opposées.
Par conséquent, la valeur totale de ce portefeuille reste inchangée. La limitation de l'appariement de la durée est que la méthode n'immunise le portefeuille que contre de petites variations de taux d'intérêt. Il est moins efficace pour les changements importants de taux d'intérêt.
Lectures connexes
Pour continuer à apprendre et à développer vos connaissances en analyse financière, nous vous recommandons vivement les ressources supplémentaires ci-dessous :
- Taux d'actualisationTaux d'actualisationEn finance d'entreprise, un taux d'actualisation est le taux de rendement utilisé pour actualiser les flux de trésorerie futurs à leur valeur actuelle. Ce taux est souvent le coût moyen pondéré du capital (WACC) d'une entreprise, taux de rendement requis, ou le taux limite que les investisseurs s'attendent à gagner par rapport au risque de l'investissement.
- Effective DurationEffective DurationEffective Duration est la sensibilité du prix d'une obligation par rapport à la courbe de rendement de référence. Une façon d'évaluer le risque d'une obligation consiste à estimer le
- Courbe de rendementCourbe de rendementLa courbe de rendement est une représentation graphique des taux d'intérêt sur la dette pour une gamme d'échéances. Il montre le rendement qu'un investisseur s'attend à gagner s'il prête son argent pendant une période donnée. Le graphique affiche le rendement d'une obligation sur l'axe vertical et le temps jusqu'à l'échéance sur l'axe horizontal.
- Durée modifiéeDurée modifiéeDurée modifiée, une formule couramment utilisée dans les évaluations des obligations, exprime la variation de la valeur d'un titre en raison d'une variation des taux d'intérêt. En d'autre
investir
-
 Devriez-vous (ou n'importe qui) acheter des Stablecoins ?
Devriez-vous (ou n'importe qui) acheter des Stablecoins ? Beaucoup ou tous les produits ici proviennent de nos partenaires qui nous paient une commission. Cest comme ça quon gagne de largent. Mais notre intégrité éditoriale garantit que les opinions de nos e...
-
 Comment les gens réagissent aux incitations en économie
Comment les gens réagissent aux incitations en économie Les prix élevés poussent les consommateurs à se tourner vers des produits moins chers. Les incitations en économie sont des facteurs qui peuvent modifier le comportement dachat des consommateurs. Il ...
-
 5 mouvements d'argent brillants que vous devriez faire le 1er janvier
5 mouvements d'argent brillants que vous devriez faire le 1er janvier Beaucoup dentre nous prennent des résolutions le jour du Nouvel An. Et, Oui, la plupart dentre nous enfreignent ces mêmes résolutions avant la fin de janvier. Mais quen est-il des mouvements dargent p...
-
 Conseils financiers pour les couples non mariés
Conseils financiers pour les couples non mariés Selon les données du recensement, 7,5 millions de couples non mariés vivaient ensemble en 2010. Alors que de nombreuses relations entre ces partenaires non mariés ne durent pas ou ne conduisent pas au...




