Comment interpoler les taux d'intérêt
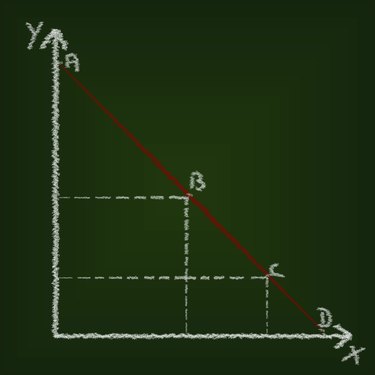 L'interpolation linéaire estime les valeurs entre les points de données.
L'interpolation linéaire estime les valeurs entre les points de données. L'interpolation est un processus mathématique pour estimer la valeur d'une variable dépendante sur la base des valeurs des variables dépendantes environnantes connues, où la variable dépendante est fonction d'une variable indépendante. Il est utilisé pour déterminer les taux d'intérêt pour des périodes qui ne sont pas publiées ou autrement mises à disposition. Dans ce cas, le taux d'intérêt est la variable dépendante, et la durée est la variable indépendante. Pour interpoler un taux d'intérêt, vous aurez besoin du taux d'intérêt d'une période plus courte et d'une période plus longue.
Étape 1
Soustraire le taux d'intérêt d'une période de temps plus courte que la période de temps du taux d'intérêt souhaité du taux d'intérêt d'une période de temps plus longue que la période de temps du taux d'intérêt souhaité. Par exemple, si vous interpolez un taux d'intérêt à 45 jours, et le taux d'intérêt à 30 jours est de 4,2242% et le taux d'intérêt à 60 jours est de 4,4855%, la différence entre les deux taux d'intérêt connus est de 0,2613 %.
Étape 2
Divisez le résultat de l'étape 1 par la différence entre les longueurs des deux périodes. Par exemple, la différence entre le délai de 60 jours et le délai de 30 jours est de 30 jours. Divisez 0,2613 pour cent par 30 jours et le résultat est 0,00871 pour cent.
Étape 3
Multipliez le résultat de l'étape 2 par la différence entre la durée du taux d'intérêt souhaité et la durée du taux d'intérêt avec la durée la plus courte. Par exemple, le taux d'intérêt souhaité est à 45 jours, et le taux d'intérêt connu le plus court est le taux à 30 jours. La différence entre 45 jours et 30 jours est de 15 jours. 15 multiplié par 0,00871 pour cent équivaut à 0,13065 pour cent.
Étape 4
Ajoutez le résultat de l'étape 3 au taux d'intérêt pour la période connue la plus courte. Par exemple, le taux d'intérêt de la période de 30 jours est de 4,2242 pour cent. La somme de 4,2242 pour cent et 0,13065 pour cent est de 4,35485 pour cent. Il s'agit de l'estimation par interpolation du taux d'intérêt à 45 jours.
Conseil
Pour vous assurer que vous suivez correctement l'équation, il peut être utile de tracer un graphique. Le graphique doit avoir un axe représentant les taux d'intérêt, avec l'autre axe représentant la durée. Tracez une ligne droite passant par les deux points représentant les taux d'intérêt connus. Si le taux d'intérêt que vous interpolez se situe en dehors de cette ligne, vous saurez que vous avez fait une erreur en cours de route.
Avertissement
L'interpolation linéaire est une estimation du taux d'intérêt d'une période donnée, et il suppose que le taux d'intérêt change sur une base linéaire entre chaque jour. En réalité, les taux d'intérêt peuvent suivre une « courbe de rendement » au lieu d'une ligne droite. L'estimation sera d'autant plus précise que la période entre les taux d'intérêt connus à partir desquels vous interpolez sera courte.
Choses dont vous aurez besoin
-
Calculatrice
-
Crayon
-
Papier
investir
-
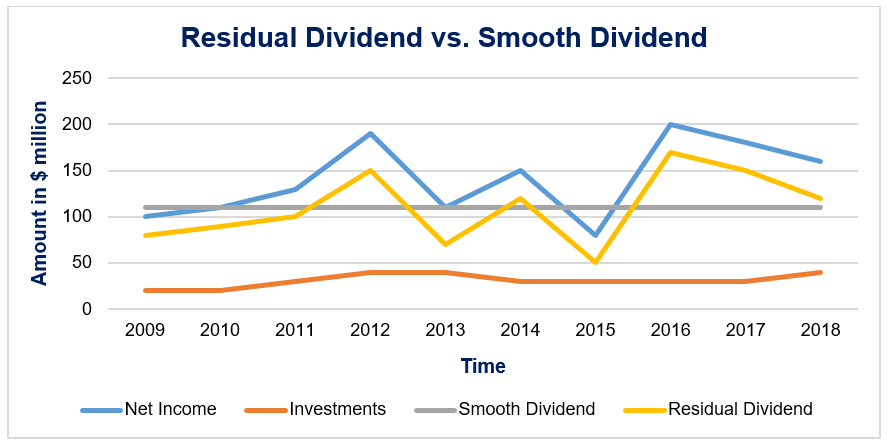 Qu'est-ce qu'une politique de dividende résiduel?
Qu'est-ce qu'une politique de dividende résiduel? Une entreprise avec une politique de dividende résiduel ne détient aucun excédent de trésorerie à un moment donné. Toutes les liquidités disponibles doivent être soit réinvesties dans lentreprise, soi...
-
 Extension de la loi sur le congé familial contre le coronavirus - La loi sur la réponse au coronavirus pour les familles d'abord
Extension de la loi sur le congé familial contre le coronavirus - La loi sur la réponse au coronavirus pour les familles d'abord La pandémie de coronavirus a posé des défis sans précédent aux États-Unis et au reste du monde. Pour aider à lutter contre bon nombre des défis financiers auxquels notre pays est confronté, Le Congrès...
-
 Si quelqu'un vous signe un chèque, pouvez-vous quand même l'encaisser ?
Si quelqu'un vous signe un chèque, pouvez-vous quand même l'encaisser ? Si quelquun vous signe un chèque, pouvez-vous quand même lencaisser ? Vous devez 100 $ à un ami, mais vous nêtes pas encore arrivé à la banque avec le chèque danniversaire que votre Nana vous a envoy...
-
 Qu'est-ce que l'intégration en aval ?
Qu'est-ce que l'intégration en aval ? Lintégration en aval est une forme dintégration verticaleIntégration verticaleUne intégration verticale, cest lorsquune entreprise étend ses opérations au sein de sa chaîne dapprovisionnement. Cela si...




