Qu'est-ce que le rendement attendu ?
Le rendement attendu d'un investissement est la valeur attendue de la distribution de probabilité des retours possibles qu'il peut fournir aux investisseurs. Le retour sur investissement est une variable inconnue qui a différentes valeurs associées à différentes probabilités. Le rendement attendu est calculé en multipliant les résultats potentiels (rendements) par les chances que chaque résultat se produise, puis calculer la somme de ces résultats (comme indiqué ci-dessous).

A court terme, le retour sur investissement peut être considéré comme une variable aléatoire Théorie de la marche aléatoire La théorie de la marche aléatoire est un modèle mathématique du marché boursier. La théorie postule que le prix des titres évolue de manière aléatoire et peut prendre n'importe quelle valeur dans une fourchette donnée. Le rendement attendu est basé sur des données historiques, qui peuvent ou non fournir une prévision fiable des rendements futurs. D'où, le résultat n'est pas garanti. Le rendement attendu est simplement une mesure des probabilités visant à montrer la probabilité qu'un investissement donné génère un rendement positif, et quel sera le retour probable.
Le but du calcul du rendement attendu d'un investissement est de fournir à un investisseur une idée du bénéfice probable par rapport au risque. Cela donne à l'investisseur une base de comparaison avec le taux de rendement sans risque. Le taux d'intérêt des bons du Trésor américain à 3 mois est souvent utilisé pour représenter le taux de rendement sans risque.
Bases de la distribution de probabilité
Pour une variable aléatoire donnée, sa distribution de probabilité est une fonction qui montre toutes les valeurs possibles qu'elle peut prendre. Elle est confinée à une certaine plage dérivée des valeurs maximales et minimales statistiquement possibles. Les distributions peuvent être de deux types :discrètes et continues. Les distributions discrètes affichent uniquement des valeurs spécifiques dans une plage donnée. Une variable aléatoire suivant une distribution continue peut prendre n'importe quelle valeur dans la plage donnée. Lancer une pièce a deux résultats possibles et est donc un exemple de distribution discrète. Une distribution de la taille des mâles adultes, qui peut prendre n'importe quelle valeur possible dans une plage donnée, est une distribution de probabilité continue.

Téléchargez le modèle gratuit
Entrez votre nom et votre e-mail dans le formulaire ci-dessous et téléchargez le modèle gratuit maintenant !
Calcul du rendement attendu pour un seul investissement
Prenons un investissement A, qui a une probabilité de 20% de donner un retour sur investissement de 15%, une probabilité de 50% de générer un rendement de 10%, et une probabilité de 30 % d'entraîner une perte de 5 %. Il s'agit d'un exemple de calcul d'une distribution de probabilité discrète pour les rendements potentiels.
Les probabilités de chaque résultat de rendement potentiel sont dérivées de l'étude des données historiques sur les rendements antérieurs de l'actif d'investissement évalué. Les probabilités énoncées, dans ce cas, pourrait être dérivé de l'étude de la performance de l'actif au cours des 10 dernières années. Supposons qu'il ait généré un retour sur investissement de 15 % pendant deux de ces 10 ans, un rendement de 10 % pendant cinq des 10 ans, et a subi une perte de 5 % pendant trois des 10 années.
Le retour sur investissement attendu A serait alors calculé comme suit :
Rendement attendu de A =0,2 (15 %) + 0,5 (10 %) + 0,3 (-5 %)
(C'est-à-dire, un 20%, ou .2, probabilité multipliée par 15%, ou .15, revenir; plus 50%, ou .5, probabilité multipliée par 10 %, ou .1, revenir; plus 30%, ou .3, probabilité d'un rendement négatif de 5%, ou -.5)
=3 % + 5 % – 1,5 %
=6,5%
Par conséquent, le rendement moyen probable à long terme de l'investissement A est de 6,5 %.
Calcul du rendement attendu d'un portefeuille
Le calcul du rendement attendu ne se limite pas aux calculs pour un seul investissement. Il peut également être calculé pour un portefeuille. Le rendement attendu d'un portefeuille d'investissement est la moyenne pondérée du rendement attendu de chacune de ses composantes. Les composants sont pondérés par le pourcentage de la valeur totale du portefeuille que chacun représente. L'examen de la moyenne pondérée des actifs du portefeuille peut également aider les investisseurs à évaluer la diversification de leur portefeuille d'investissement.
Pour illustrer le rendement attendu d'un portefeuille d'investissement, supposons que le portefeuille est composé d'investissements dans trois actifs - X, Oui, et Z. 2 $, 000 est investi dans X, 5 $, 000 investis dans Y, et 3 $, 000 est investi dans Z. Supposons que les rendements attendus pour X, Oui, et Z ont été calculés et trouvés à 15 %, dix%, et 20%, respectivement. Sur la base des investissements respectifs dans chaque élément d'actif, le rendement attendu du portefeuille peut être calculé comme suit :
Rendement attendu du portefeuille =0,2 (15 %) + 0,5 (10 %) + 0,3 (20 %)
=3% + 5% + 6%
=14%
Ainsi, le rendement attendu du portefeuille est de 14 %.
Notez que bien que la moyenne simple du rendement attendu des composantes du portefeuille soit de 15 % (la moyenne de 10 %, 15%, et 20%), le rendement attendu du portefeuille de 14 % est légèrement inférieur à cette moyenne simple. Cela est dû au fait que la moitié du capital de l'investisseur est investie dans l'actif avec le rendement attendu le plus faible .
Analyser le risque d'investissement
En plus de calculer le rendement attendu, les investisseurs doivent également tenir compte des caractéristiques de risque des actifs d'investissement. Cela permet de déterminer si les composants du portefeuille sont correctement alignés sur la tolérance au risque et les objectifs d'investissement de l'investisseur.
Par exemple, supposons que deux composantes du portefeuille ont affiché les rendements suivants, respectivement, au cours des cinq dernières années :
Composante A du portefeuille :12 %, 2%, 25%, -9%, dix%
Composante B du portefeuille :7 %, 6%, 9%, 12%, 6%
Le calcul du rendement attendu pour les deux composantes du portefeuille donne le même chiffre :un rendement attendu de 8 %. Cependant, lorsque chaque composant est examiné pour le risque, sur la base des écarts d'une année sur l'autre par rapport aux rendements moyens attendus, vous constatez que le composant de portefeuille A comporte cinq fois plus de risque que le composant de portefeuille B (A a un écart type de 12,6 %, alors que l'écart type de B n'est que de 2,6%. L'écart type représente le niveau de variance qui se produit par rapport à la moyenne.
Le rôle de la tolérance au risque et d'autres facteurs
Le concept de rendement attendu fait partie du processus global d'évaluation d'un investissement potentiel. Bien que les analystes de marché aient mis au point des formules mathématiques simples pour calculer le rendement attendu, les investisseurs individuels peuvent tenir compte de facteurs supplémentaires lors de la constitution d'un portefeuille de placement qui correspond bien à leurs objectifs de placement personnels et à leur niveau de tolérance au risque.
Par exemple, un investisseur peut tenir compte des conditions économiques ou du climat d'investissement spécifiques qui prévalent. En période d'extrême incertitude, les investisseurs sont enclins à se tourner vers des investissements généralement plus sûrs et moins volatils, même si l'investisseur est généralement plus tolérant au risque. Ainsi, un investisseur peut se détourner des actions présentant des écarts types élevés par rapport à leur rendement moyen, même si leurs calculs montrent que l'investissement offre un excellent rendement moyen.
Il est également important de garder à l'esprit que le rendement attendu est calculé en fonction des performances passées d'une action. Cependant, si un investisseur a des connaissances sur une entreprise qui le portent à croire que, aller de l'avant, il surperformera considérablement par rapport à ses normes historiques, ils pourraient choisir d'investir dans une action qui ne semble pas très prometteuse en se basant uniquement sur les calculs de rendement attendu. Une mesure financière utile à considérer en plus du rendement attendu est le ratio de retour sur investissement (ROI)Formule de ROI (retour sur investissement)Le retour sur investissement (ROI) est un ratio financier utilisé pour calculer l'avantage qu'un investisseur recevra par rapport à ses coût d'investissement. Il est le plus souvent mesuré comme le revenu net divisé par le coût en capital initial de l'investissement. Plus le rapport est élevé, plus l'avantage gagné est important., un ratio de rentabilité qui compare directement la valeur des bénéfices accrus qu'une entreprise a générés grâce à l'investissement en capital dans son entreprise.
Bien qu'il ne s'agisse pas d'un prédicteur garanti de la performance des actions, la formule de rendement attendu s'est avérée être un excellent outil d'analyse qui aide les investisseurs à prévoir les rendements probables des investissements et à évaluer le risque et la diversification du portefeuille.
Lecture connexe
CFI est le fournisseur mondial officiel du programme de certification Financial Modeling and Valuation Analyst. Inscrivez-vous aujourd'hui !. Pour continuer à apprendre et à construire votre carrière en tant qu'analyste financier, ces ressources supplémentaires seront utiles :
- Investir :Guide du débutantInvestissement :Guide du débutantLe guide Investir pour les débutants de CFI vous apprendra les bases de l'investissement et comment commencer. En savoir plus sur les différentes stratégies et techniques de trading
- Capital Asset Pricing ModelCapital Asset Pricing Model (CAPM)Le Capital Asset Pricing Model (CAPM) est un modèle qui décrit la relation entre le rendement attendu et le risque d'un titre. La formule CAPM montre que le rendement d'un titre est égal au rendement sans risque plus une prime de risque, sur la base de la version bêta de ce titre
- Analyse technique :Guide du débutantAnalyse technique - Guide du débutantL'analyse technique est une forme d'évaluation des investissements qui analyse les prix passés pour prédire l'évolution future des prix. Les analystes techniques estiment que les actions collectives de tous les acteurs du marché reflètent avec précision toutes les informations pertinentes, et donc, attribuer continuellement une juste valeur marchande aux titres.
- Basis RiskBasis RiskBasis Risk est le risque que le prix à terme ne bouge pas normalement, corrélation constante avec le prix de l'actif sous-jacent, afin d'annuler l'efficacité d'une stratégie de couverture pour minimiser l'exposition d'un trader à une perte potentielle. Le risque de base est accepté dans le but de couvrir le risque de prix.
investir
- Actions à dividendes :qu'est-ce que c'est et comment y investir
- Comment investir dans des actions - Un guide simple
- Quel type de compte de retraite vous convient le mieux ?
- Qu'est-ce qu'une introduction en bourse ? Un aperçu des offres publiques initiales
- Qu'est-ce qu'un fonds d'actions ?
- Jeunes investisseurs :n'attendez pas ! Commencez à investir maintenant
-
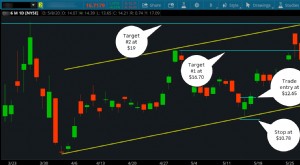 Demandez au trader :comment placez-vous des swing trades avec plus d'un objectif de prix ?
Demandez au trader :comment placez-vous des swing trades avec plus d'un objectif de prix ? Lobjectif dun swing trade est généralement de capturer des rendements en quelques jours. Les swing traders connaissent généralement à lavance leurs points dentrée et de sortie. Ils ont décidé où un co...
-
 Que savoir si vous habitez dans l'un de ces 10 principaux points chauds de vol de voiture
Que savoir si vous habitez dans l'un de ces 10 principaux points chauds de vol de voiture Un nouveau rapport du NICB a révélé que le vol dautomobiles augmente à léchelle nationale, et le problème est encore pire dans certains points chauds. Avec laugmentation des vols dautomobiles, il est ...
-
 PastCast T3 2021 :trafic à venir
PastCast T3 2021 :trafic à venir Voici tout ce que vous devez savoir. (Si vous êtes pressé.) Sur le front du COVID, Lété 2021 a été défini par une nouvelle variante effrayante connue sous le nom de Delta. Rétablissement régiona...
-
 Quelle est la différence entre les familles à faible revenu et les familles pauvres?
Quelle est la différence entre les familles à faible revenu et les familles pauvres? Les lignes directrices sur la pauvreté et le faible revenu sont des mesures utilisées par le gouvernement fédéral pour déterminer si vous êtes admissible à certains types daide publique. Les personne...




