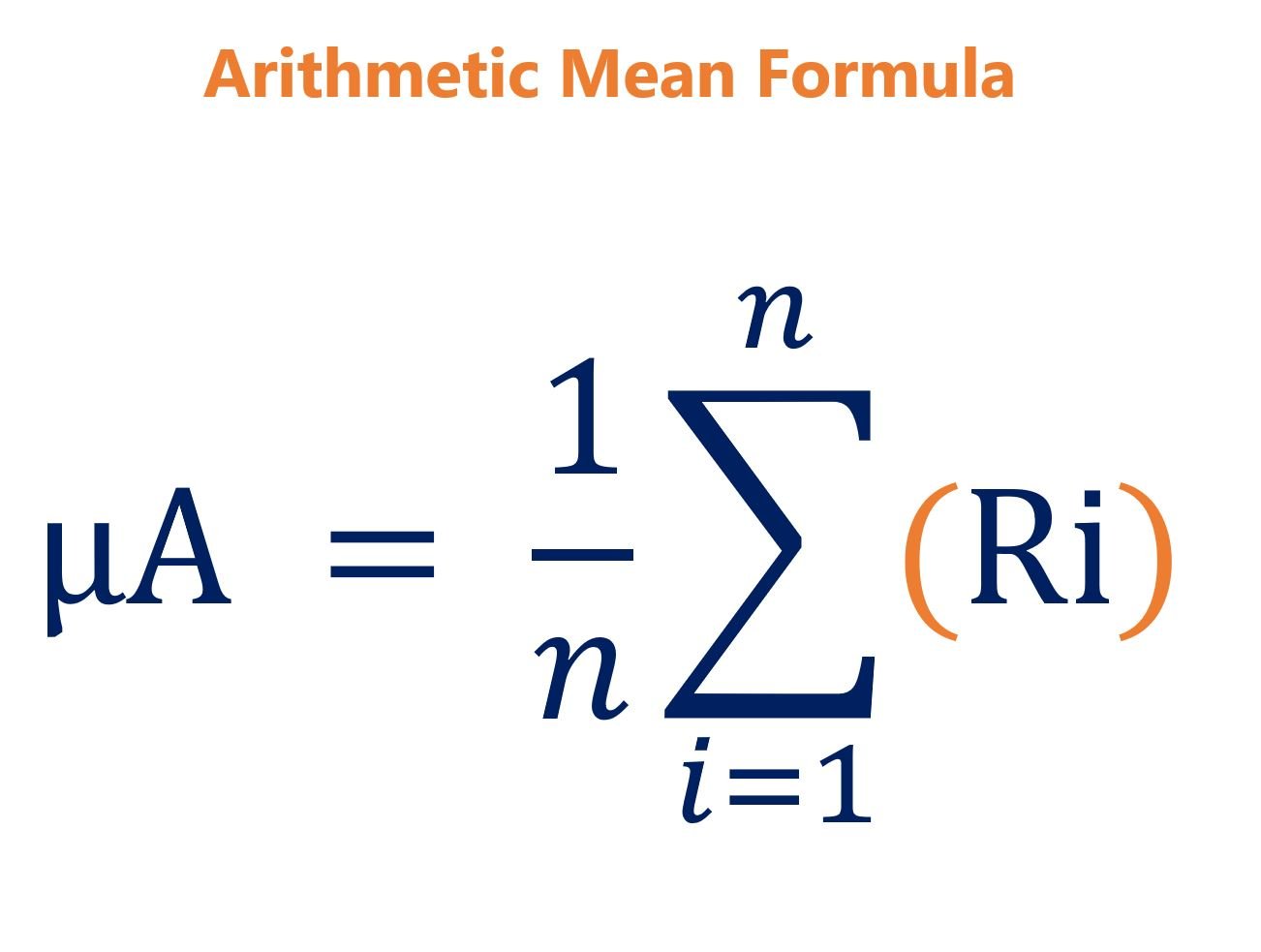Qu'est-ce que le rapport de Sharpe ?
Nommé d'après l'économiste américain, William Sharpe, le ratio de Sharpe (ou indice de Sharpe ou ratio de Sharpe modifié) est couramment utilisé pour évaluer la performance d'un investissement en ajustant son risque.
Plus le rapport est élevé, plus le retour sur investissement est élevé par rapport au montant du risque pris, Et ainsi, meilleur est l'investissement. Le ratio peut être utilisé pour évaluer une seule action ou investissement, ou un portefeuille entier.
Formule du rapport de Sharpe
Ratio de Sharpe =(Rx – Rf) / StdDev Rx
Où:
- Rx =Rendement attendu du portefeuille
- Rf =taux de rendement sans risque
- StdDev Rx =Écart type du rendement du portefeuille (ou, volatilité)

Seuils de notation du rapport de Sharpe :
- Moins que 1: Mauvais
- 1 - 1,99 : Adéquat/bien
- 2 - 2,99 : Très bon
- Supérieur à 3 : Excellent
Qu'est-ce que cela signifie vraiment?
Il s'agit de maximiser les rendements et de réduire la volatilité. Si un investissement avait un rendement annuel de seulement 10 % mais n'avait aucune volatilité, il aurait un rapport de Sharpe infini (ou indéfini).
Bien sûr, il est impossible d'avoir une volatilité nulle, même avec une obligation d'État (les prix montent et descendent). À mesure que la volatilité augmente, le rendement attendu doit augmenter de manière significative pour compenser ce risque supplémentaire.
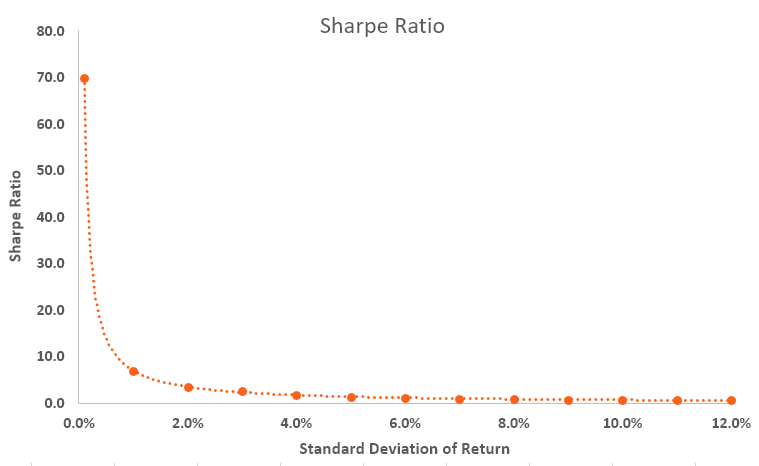
Le ratio de Sharpe révèle le rendement moyen des investissements, moins le taux de rendement sans risque, divisé par l'écart type des rendements de l'investissement. Vous trouverez ci-dessous un résumé de la relation exponentielle entre la volatilité des rendements et le ratio de Sharpe.
Téléchargez le modèle gratuit
Entrez votre nom et votre e-mail dans le formulaire ci-dessous et téléchargez le modèle gratuit maintenant !
Application de l'indice de Sharpe
Un portefeuille d'investissement peut être composé d'actions, obligations, ETF, dépôts, métaux précieux, ou d'autres titres. Chaque titre a son propre niveau de risque-rendement sous-jacent qui influence le ratio.
Par exemple, supposons qu'un gestionnaire de fonds spéculatifs a un portefeuille d'actions avec un ratio de 1,70. Le gérant décide d'ajouter quelques matières premières pour diversifier et modifier la composition à 80/20, actions/matières premières, ce qui pousse le ratio de Sharpe jusqu'à 1,90.
Bien que l'ajustement du portefeuille puisse augmenter le niveau global de risque, ça fait monter le ratio, indiquant ainsi une situation risque/rendement plus favorable. Si le changement de portefeuille fait baisser le ratio, puis l'ajout de portefeuille, tout en offrant potentiellement des rendements attractifs, serait évalué par de nombreux analystes financiers comme comportant un niveau de risque inacceptable, et le changement de portefeuille ne serait pas effectué.
Exemple de l'indice de Sharpe
Considérons deux gestionnaires de fonds, A et B. Le gestionnaire A a un rendement du portefeuille de 20 % tandis que B a un rendement de 30 %. La performance du S&P 500 est de 10 %. Bien qu'il semble que B soit plus performant en termes de rendement, quand on regarde le ratio de Sharpe, il s'avère que A a un rapport de 2 alors que le rapport de B n'est que de 0,5.
Les chiffres signifient que B prend beaucoup plus de risques que A, ce qui peut expliquer ses rendements plus élevés, mais cela signifie également qu'il a plus de chances de subir éventuellement des pertes.
Rapport de Sharpe géométrique par rapport au rapport de Sharpe modifié
Le ratio de Sharpe géométrique est la moyenne géométrique des rendements excédentaires composés divisé par l'écart-type de ces rendements composésTaux de croissance composéLe taux de croissance composé est une mesure utilisée spécifiquement dans les contextes d'affaires et d'investissement, qui indique le taux de croissance sur plusieurs périodes. C'est une mesure de la croissance constante d'une série de données. Le plus grand avantage du taux de croissance composé est que la métrique prend en considération l'effet composé. Retour.
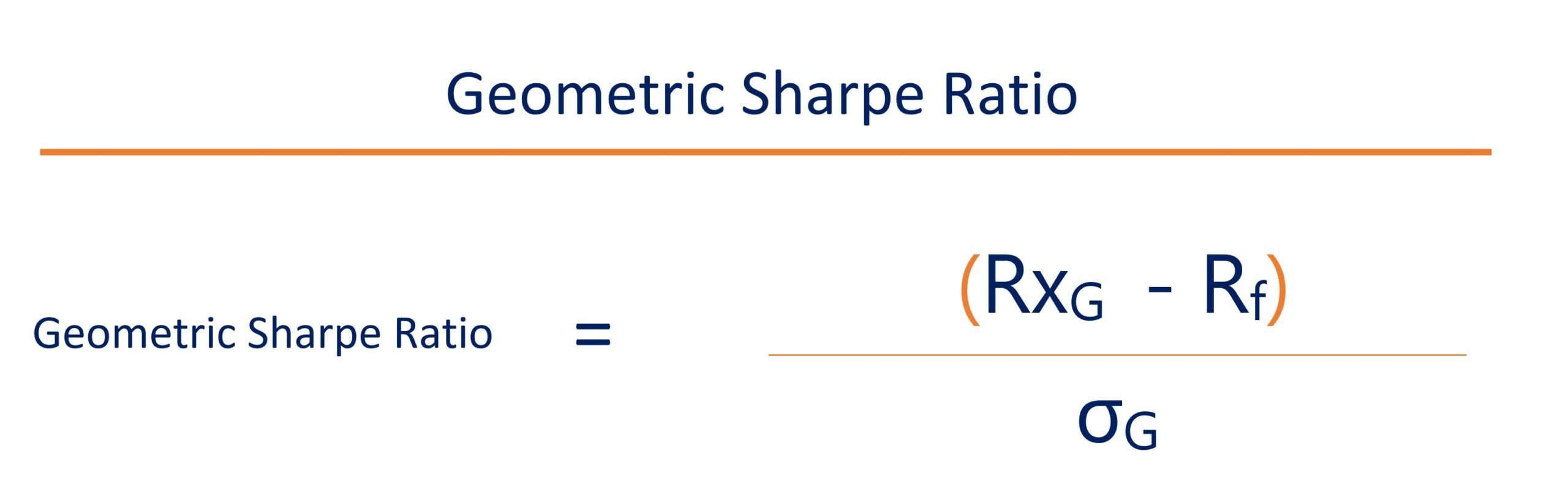
Où:
- Rx
g =Moyenne géométrique des rendements composés - Rf =taux de rendement sans risque
- ??
g =Écart-type des rendements composés
Étant donné que l'indice de Sharpe tient déjà compte du risque dans le dénominateur, utilisant la moyenne géométriqueModèle de moyenne géométriqueCe modèle de moyenne géométrique vous aide à comparer les options d'investissement en calculant la valeur finale des investissements à l'aide de la moyenne géométrique. La moyenne géométrique est la croissance moyenne d'un investissement calculée en multipliant n variables puis en prenant la n racine carrée. En d'autres termes, c'est le rendement moyen d'un investissement qui compterait deux fois le risque. Avec la volatilité, la moyenne géométrique sera toujours inférieure à sa moyenne arithmétique.
En plus de ça, le ratio géométrique de Sharpe prend en compte les rendements réels et est un ratio plus prudent. Par conséquent, la principale différence entre le ratio de Sharpe modifié et le ratio de Sharpe géométrique serait la moyenne des rendements excédentaires calculés à l'aide des formules ci-dessous :


Remarque :Pour une comparaison des rendements de pomme à pomme, le Geometric Sharpe Ratio d'un portefeuille doit toujours être comparé avec le Geometric Sharpe Ratio d'autres portefeuilles.
Ressources additionnelles
Merci d'avoir lu cet article sur la mesure du rendement ajusté en fonction du risque. La mission de CFI est de vous aider à faire avancer votre carrière en finance d'entreprise. Pour continuer à apprendre et à progresser dans votre carrière, nous vous recommandons ces ressources supplémentaires de la FCI :
- Taux de rendement comptable (ARR) ARR - Taux de rendement comptable Le taux de rendement comptable (ARR) est le revenu net moyen qu'un actif devrait générer divisé par son coût en capital moyen, exprimé comme
- Risque et rendementRisque et rendementDans l'investissement, le risque et le rendement sont fortement corrélés. Des retours potentiels sur investissement accrus vont généralement de pair avec un risque accru. Les différents types de risques incluent le risque spécifique au projet, risque spécifique à l'industrie, risque concurrentiel, risque international, et le risque de marché.
- Taux de rentabilité interne (TRI)Taux de rentabilité interne (TRI) Le taux de rentabilité interne (TRI) est le taux d'actualisation qui met à zéro la valeur actuelle nette (VAN) d'un projet. En d'autres termes, il s'agit du taux de rendement annuel composé attendu qui sera obtenu sur un projet ou un investissement.
- Guide de modélisation financièreGuide de modélisation financière gratuitCe guide de modélisation financière couvre les conseils Excel et les meilleures pratiques sur les hypothèses, Conducteurs, prévision, reliant les trois énoncés, Analyse DCF, Suite
la finance
-
 Une astuce simple pour que votre soirée en vaille la peine
Une astuce simple pour que votre soirée en vaille la peine Crédit dimage:@ marcpurnomo/Twenty20 Sortir était plus amusant avant, et tu ne limagines pas. De nouvelles recherches ont montré pourquoi, et a proposé la solution parfaite. Vous nallez probablement ...
-
 Passer sans voiture :une façon extrême d'économiser
Passer sans voiture :une façon extrême d'économiser En Amérique, cest presque un sacrilège de suggérer cela, même chez les écologistes frugaux, mais lun des meilleurs moyens de vous faire économiser beaucoup dargent est de vous débarrasser de votre voi...
-
 Comment épargner pour la retraite à 30 ans
Comment épargner pour la retraite à 30 ans Dans la trentaine, les responsabilités reprennent. Vous êtes susceptible d’acheter votre première maison et d’agrandir votre famille. Mariage, une hypothèque et de petites bouches à nourrir peuvent ép...
-
 Examen de l'amélioration 2021
Examen de l'amélioration 2021 Amélioration Note globale 9.5 Résultat final Avec plus de 8 milliards de dollars sous gestion, Betterment est une entreprise innovante qui facilite linvestissement avec des outils auparavant r...