Qu'est-ce que Vomma ?

Vomma est une option grecque qui représente la sensibilité de vega au changement de la volatilité impliciteVolatilité implicite (IV)La volatilité implicite - ou simplement IV - utilise le prix d'une option pour calculer ce que le marché dit de la volatilité future de option. C'est la dérivée seconde de la valeur de l'option par rapport à la volatilité. Ainsi, il est également connu comme un grec de second ordre. D'autres Grecs de second ordre incluent gamma, vanna, veta, etc.

Sommaire

• Vomma est un grec de second ordre qui mesure la sensibilité de vega au changement de la volatilité implicite de l'actif sous-jacent d'une option.
• Un vomma positif signifie que le vega augmente (diminue) lorsque la volatilité augmente (diminue); un vomma négatif signifie que le vega diminue (augmente) lorsque la volatilité augmente (diminue).
• Vomma aide à estimer la variation du prix de l'option avec plus de précision pour les changements significatifs du niveau de volatilité.

Vomma et Véga

Une option fait référence à un type de dérivé financier qui offre à l'acheteur un droit, au lieu d'une obligation, acheter l'actif sous-jacent à un prix prédéterminé. Entreprises, investisseurs individuels, et les instituts d'investissement détiennent des options comme méthode pour couvrir les risques ou générer des bénéfices.

De nombreux facteurs influent sur la valeur d'une option. Ils comprennent le prix et la volatilité de l'actif sous-jacent, délai d'exécution, taux d'intérêt sans risqueTaux sans risqueLe taux de rendement sans risque est le taux d'intérêt qu'un investisseur peut s'attendre à gagner sur un investissement qui ne comporte aucun risque. En pratique, le taux sans risque est communément considéré comme égal aux intérêts payés sur un bon du Trésor public à 3 mois, généralement l'investissement le plus sûr qu'un investisseur puisse faire., etc.

Les grecs du premier ordre sont utilisés pour mesurer la sensibilité des valeurs d'options aux changements des facteurs. L'un de ces Grecs est vega, qui montre la variation en pourcentage du prix d'une option, la volatilité implicite de l'actif sous-jacent évolue de 1%.

Les investisseurs et les entreprises sont plus disposés à acheter des options pour couvrir les risques lorsque les actifs sont plus volatils, ce qui entraîne une hausse des prix des options, et vice versa. Par conséquent, pour les options d'achat et de vente, les positions longues ont toujours un vega positif, et les positions courtes ont toujours un vega négatif.

Les Grecs du second ordre calculent la sensibilité des Grecs du premier ordre au changement des facteurs correspondants. Vomma est un grec de second ordre qui mesure le changement de vega en réponse au changement de volatilité. Aussi connue sous le nom de convexité vega, vomma prend la dérivée seconde de la valeur à la volatilité d'une option

Si une option a un vomma positif, son vega augmente (diminue) lorsque la volatilité implicite augmente (baisse). Si le vomi est négatif, le vega augmente (diminue) à mesure que la volatilité diminue (augmente).

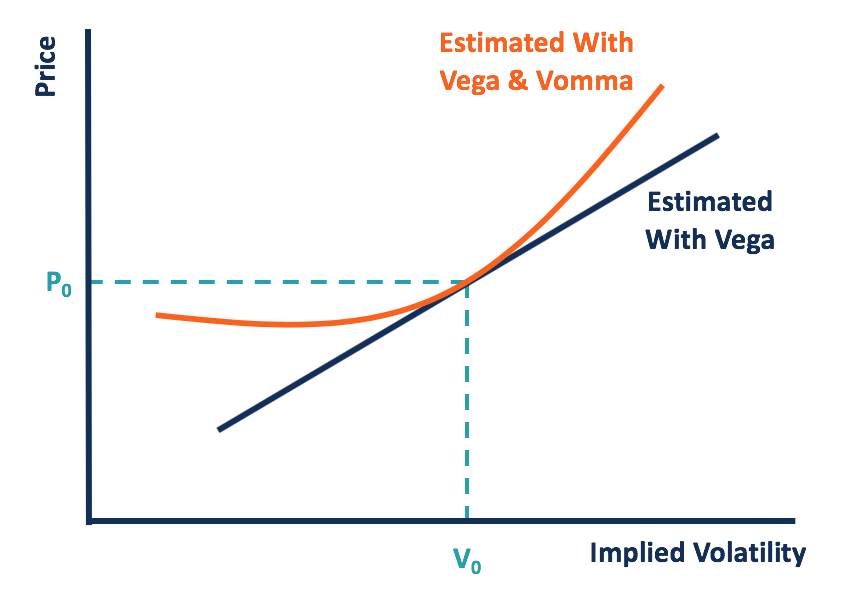
Comme vega suppose une relation linéaire entre le prix et la volatilité d'une option, vomma montre la relation dans un convexe. Cela signifie qu'en utilisant vega seul, des variations plus importantes de la volatilité implicite entraînent des écarts plus importants entre la variation de prix estimée et le mouvement de prix réel.

En combinant vega et vomma, les commerçants peuvent estimer le mouvement des prix avec plus de précision, en particulier pour les changements substantiels de la volatilité.

Supposons qu'une option soit positive à la fois dans vomma et vega. Lorsque la volatilité augmente (baisse), l'augmentation (baisse) de prix estimée avec vega est inférieure à celle estimée avec vega et vomma. Ainsi, le prix de l'option est toujours sous-estimé en n'utilisant que vega, par rapport à la prise en compte de vomma.

Formule de Vomma

Vomma peut être calculé comme la dérivée de vega à la volatilité implicite, ou le second dérivé de la valeur de l'option à la volatilité.

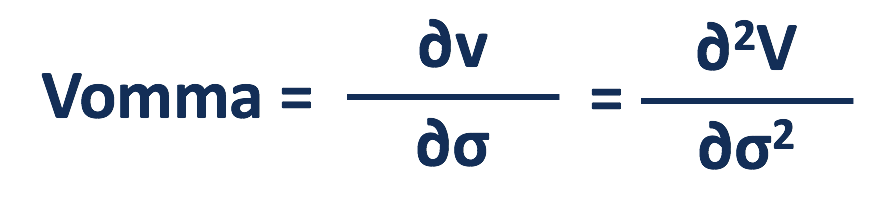
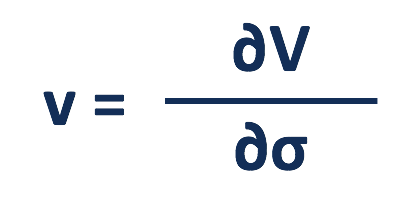
Où:

v =Véga

V =valeur de l'option

?? =Volatilité implicite de l'actif sous-jacent

Vomma calcule la variation en pourcentage de vega pour chaque variation en pourcentage de la volatilité implicite.

Par exemple, une option d'achat a un vega de 5 et un vomma de 2. Cela signifie que lorsque la volatilité implicite de l'actif sous-jacent augmente de 1%, le vega augmentera de 2%, et ainsi la valeur de l'option augmentera de plus de 5%.

Caractéristiques de Vomma

Vega et vomma sont à la fois positifs pour les positions longues et négatifs pour les positions courtes, peu importe qu'il s'agisse d'un call ou d'un putOptions :Calls and PutsUne option est un contrat dérivé qui donne à son détenteur le droit, mais pas l'obligation, acheter ou vendre un actif à une certaine date à un prix spécifié. Pour les positions longues, vega est toujours positif, et plus l'option est proche de la monnaie (ATM), plus le vega est haut. Pour les positions courtes, vega est toujours négatif et est le plus bas lorsque l'option est ATM.

Aussi, une option non-ATM ressemble plus à une option ATM lorsqu'elle a une volatilité implicite plus élevée. D'où, plus la volatilité implicite est grande, plus le vega est élevé pour les positions longues, ce qui indique un vomi positif.

Il en est de même pour les positions courtes, qu'une augmentation de la volatilité implicite entraîne une baisse de vega, ce qui indique un vomma négatif. Un vega s'approche de son niveau le plus élevé ou le plus bas à un rythme décélérant, en gardant les autres caractéristiques constantes, les options non-ATM ont un vomma plus élevé que les options à parité.

Vomma &Ultima

Ultima mesure la variation en pourcentage du vomma pour chaque variation en pourcentage de la volatilité. C'est un grec de troisième ordre et peut être calculé comme la dérivée troisième de la valeur de l'option par rapport à la volatilité implicite.

Les traders ont tendance à rechercher une augmentation du volume dans les positions longues et une diminution du volume dans les positions courtes. Ultima aide à déterminer si le vomma augmentera ou diminuera lorsque la volatilité change. Un ultima positif indique une augmentation du vomma lorsque la volatilité augmente et une diminution du vomma lorsque la volatilité diminue.

Apprendre encore plus

CFI est le fournisseur officiel de la page mondiale du programme Commercial Banking &Credit Analyst (CBCA)™ - CBCAGet obtenez la certification CBCA™ de CFI et devenez Commercial Banking &Credit Analyst. Inscrivez-vous et faites progresser votre carrière grâce à nos programmes et cours de certification. programme de certification, conçu pour aider quiconque à devenir un analyste financier de classe mondiale. Pour continuer à faire avancer votre carrière, les ressources supplémentaires de la FCI ci-dessous seront utiles :

• À l'argent (ATM) À l'argent (ATM) À l'argent (ATM) décrit une situation dans laquelle le prix d'exercice d'une option est égal au prix actuel du marché de l'actif sous-jacent. C'est une conception de
• Stock OptionStock OptionUne stock-option est un contrat entre deux parties qui donne à l'acheteur le droit d'acheter ou de vendre des actions sous-jacentes à un prix prédéterminé et dans un délai spécifié. Un vendeur d'options d'achat d'actions est appelé un vendeur d'options, où le vendeur reçoit une prime du contrat acheté par l'acheteur d'options d'achat d'actions.
• Vega (ν)Vega (ν)Vega est une mesure de sensibilité utilisée pour évaluer les options. C'est la sensibilité d'un prix d'option à une variation de 1% de la volatilité de l'actif sous-jacent
• Positions longues et courtesPositions longues et courtesEn investissement, les positions longues et courtes représentent des paris directionnels par les investisseurs qu'un titre augmentera (lorsqu'il est long) ou baissera (lorsqu'il sera court). Dans le négoce d'actifs, un investisseur peut prendre deux types de positions :longues et courtes. Un investisseur peut soit acheter un actif (aller long), ou le vendre (aller à découvert).