Qu'est-ce que le modèle Black-Scholes-Merton ?
Le modèle Black-Scholes-Merton (BSM) est un modèle de tarification pour les instruments financiers. Il est utilisé pour la valorisation des stock-options. Le modèle BSM est utilisé pour déterminer les justes prix des options d'achat d'actions sur la base de six variables :volatilitéVolatilitéLa volatilité est une mesure du taux de fluctuations du prix d'un titre au fil du temps. Il indique le niveau de risque associé aux variations de prix d'un titre. Les investisseurs et les traders calculent la volatilité d'un titre pour évaluer les variations passées des cours, taper, cours de l'action sous-jacente, prix d'exercicePrix d'exerciceLe prix d'exercice est le prix auquel le titulaire de l'option peut exercer l'option d'achat ou de vente d'un titre sous-jacent, cela dépend de, temps, et taux sans risque. Il repose sur le principe de couverture et vise à éliminer les risques liés à la volatilité des actifs sous-jacents et des stock-options.
L'équation de Black-Scholes-Merton
Le modèle de Black-Scholes-Merton peut être décrit comme une équation aux dérivées partielles du second ordre.
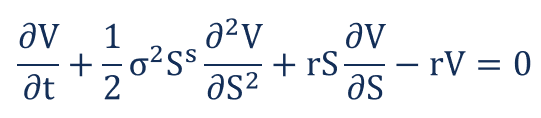
L'équation décrit le prix des options d'achat d'actions au fil du temps.
Tarification d'une option d'appel
Le prix d'une option d'achat C est donné par la formule suivante :
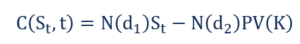
Où:
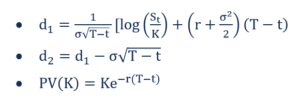
Tarification d'une option de vente
Le prix d'une option de vente P est donné par la formule suivante :
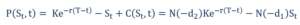
Où:
- N – Fonction de distribution cumulative de la distribution normale standard. Il représente une distribution normale standard avec moyenne =0 et écart type =1
- T-t – Délai de maturité (en années)
- S
t – Prix spot de l'actif sous-jacent - K – Prix d'exercice
- r - Taux sans risque
- ?? – Volatilité des rendements de l'actif sous-jacent
Hypothèses du modèle Black-Scholes-Merton
- Distribution lognormale :Le modèle de Black-Scholes-Merton suppose que les cours des actions suivent une distribution lognormale basée sur le principe que les prix des actifs ne peuvent pas prendre une valeur négative; ils sont bornés par zéro.
- Pas de dividendes :Le modèle BSM suppose que les actions ne versent aucun dividende ou rendement.
- Date d'expiration :Le modèle suppose que les options ne peuvent être exercées qu'à leur date d'expiration ou d'échéance. D'où, il n'évalue pas avec précision les options américaines. Il est largement utilisé sur le marché européen des options.
- Marche aléatoire :Le marché boursier est très volatil, et donc, un état de marche aléatoire Théorie de la marche aléatoire La théorie de la marche aléatoire est un modèle mathématique du marché boursier. La théorie postule que le prix des titres évolue de manière aléatoire, car la direction du marché ne peut jamais vraiment être prédite.
- Marché sans friction :Pas de frais de transaction, y compris la commission et le courtage, est supposé dans le modèle BSM.
- Taux d'intérêt sans risque :Les taux d'intérêt sont supposés constants, faisant ainsi de l'actif sous-jacent un actif sans risque.
- Distribution normale :Les rendements boursiers sont normalement distribués. Cela implique que la volatilité du marché est constante dans le temps.
- Pas d'arbitrage :Il n'y a pas d'arbitrage. Il évite l'opportunité de faire un profit sans risque.
Limites du modèle Black-Scholes-Merton
- Limité au marché européen :Comme mentionné précédemment, le modèle Black-Scholes-Merton est un déterminant précis des prix des options européennes. Il n'évalue pas avec précision les options d'achat d'actions aux États-Unis. C'est parce qu'il part du principe que les options ne peuvent être exercées qu'à leur date d'expiration/d'échéance.
- Taux d'intérêt sans risque :Le modèle BSM suppose des taux d'intérêt constants, mais ce n'est presque jamais la réalité.
- Hypothèse d'un marché sans friction :Le trading s'accompagne généralement de frais de transaction tels que les frais de courtage, commissionCommissionCommission fait référence à la rémunération versée à un employé après avoir terminé une tâche, lequel est, souvent, vendre un certain nombre de produits ou de services, etc. Cependant, le modèle Black Scholes Merton suppose un marché sans friction, ce qui signifie qu'il n'y a pas de frais de transaction. Ce n'est presque jamais la réalité sur le marché commercial.
- Aucun retour :Le modèle BSM suppose qu'il n'y a aucun rendement associé aux options d'achat d'actions. Il n'y a ni dividendes ni intérêts créditeurs. Cependant, ce n'est pas le cas sur le marché commercial actuel. L'achat et la vente d'options sont principalement axés sur les rendements.
Davantage de ressources
CFI propose la certification Financial Modeling &Valuation Analyst (FMVA)™ Devenez un Certified Financial Modeling &Valuation Analyst (FMVA)® La certification Financial Modeling and Valuation Analyst (FMVA)® de CFI vous aidera à acquérir la confiance dont vous avez besoin dans votre carrière en finance. Inscrivez-vous aujourd'hui ! programme de certification pour ceux qui cherchent à faire passer leur carrière au niveau supérieur. Pour continuer à apprendre et à progresser dans votre carrière, les ressources suivantes vous seront utiles :
- Rendement composé en continuRendement composé en continuLe rendement composé en continu est ce qui se produit lorsque les intérêts gagnés sur un investissement sont calculés et réinvestis dans le compte pendant un nombre infini de périodes. Les intérêts sont calculés sur le montant principal et les intérêts accumulés sur les périodes données
- Options :Calls et PutsOptions :Calls et PutsUne option est un contrat dérivé qui donne à son détenteur le droit, mais pas l'obligation, acheter ou vendre un actif à une certaine date à un prix spécifié.
- Taux sans risqueTaux sans risqueLe taux de rendement sans risque est le taux d'intérêt qu'un investisseur peut s'attendre à gagner sur un investissement qui ne comporte aucun risque. En pratique, le taux sans risque est communément considéré comme égal aux intérêts payés sur un bon du Trésor public à 3 mois, généralement l'investissement le plus sûr qu'un investisseur puisse faire.
- Prix au comptantPrix au comptantLe prix au comptant est le prix actuel du marché d'un titre, devise, ou un produit disponible pour être acheté/vendu pour un règlement immédiat. En d'autres termes, c'est le prix auquel les vendeurs et les acheteurs évaluent un actif en ce moment.
investir
- 10 conseils d'épargne et d'investissement pour tous les âges
- Définition d'une entreprise de brique et de mortier
- Investir avec votre conjoint ou partenaire :comment commencer
- IRA traditionnel vs Roth IRA :qu'est-ce qui vous convient le mieux ?
- Qu'est-ce que le prêt de titres ?
- Qu'est-ce que la moitié du stock ?
-
 Comment calculer la valeur des actions par action
Comment calculer la valeur des actions par action Apprenez à calculer le prix par action de vos investissements boursiers. Lorsque vous investissez en bourse, vous voulez maîtriser certaines équations mathématiques de base qui vous permettront de dé...
-
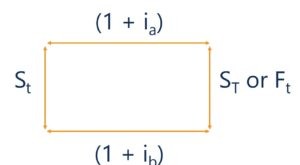 Qu'est-ce que la parité des taux d'intérêt (IRP) ?
Qu'est-ce que la parité des taux d'intérêt (IRP) ? La parité des taux dintérêt (IRP) est une théorie concernant la relation entre le taux de change au comptantPrix au comptantLe prix au comptant est le prix actuel du marché dun titre, devise, ou un pr...
-
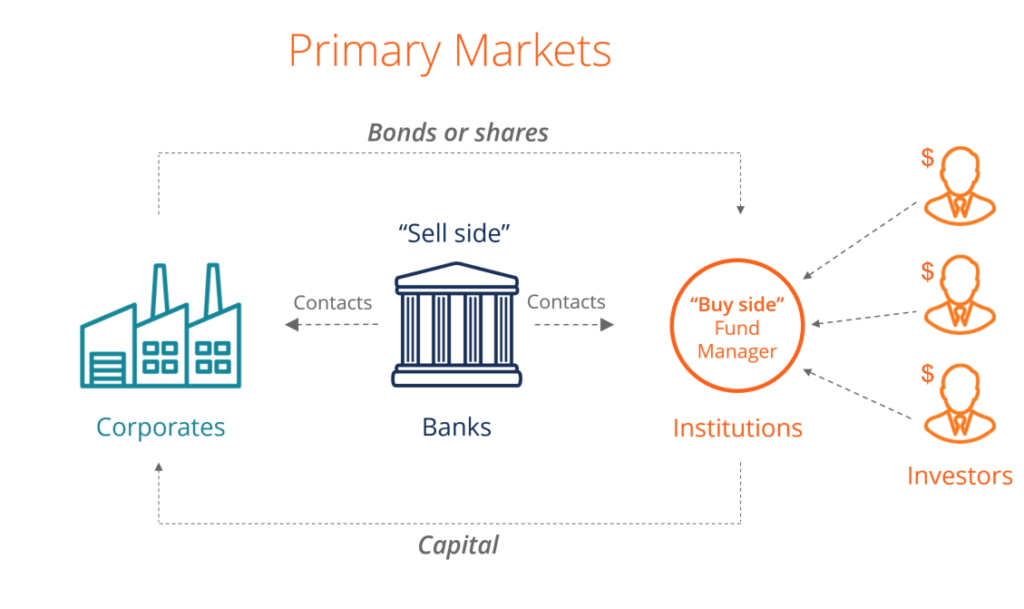 Qu'est-ce que le marché primaire ?
Qu'est-ce que le marché primaire ? Le marché primaire est le marché financier où se trouvent les nouveaux titresTitres publicsTitres publics, ou valeurs mobilières, sont des investissements qui sont ouvertement ou facilement négociés s...
-
Comment exploiter votre plan 529 pour payer les frais de scolarité
Le régime dépargne-études 529 est lun des meilleurs moyens de mettre de largent de côté pour les études collégiales de vos enfants. Le plan offre une foule de fonctionnalités qui en font une option at...




