Hétéroscédasticité

Qu'est-ce que l'hétéroscédasticité?

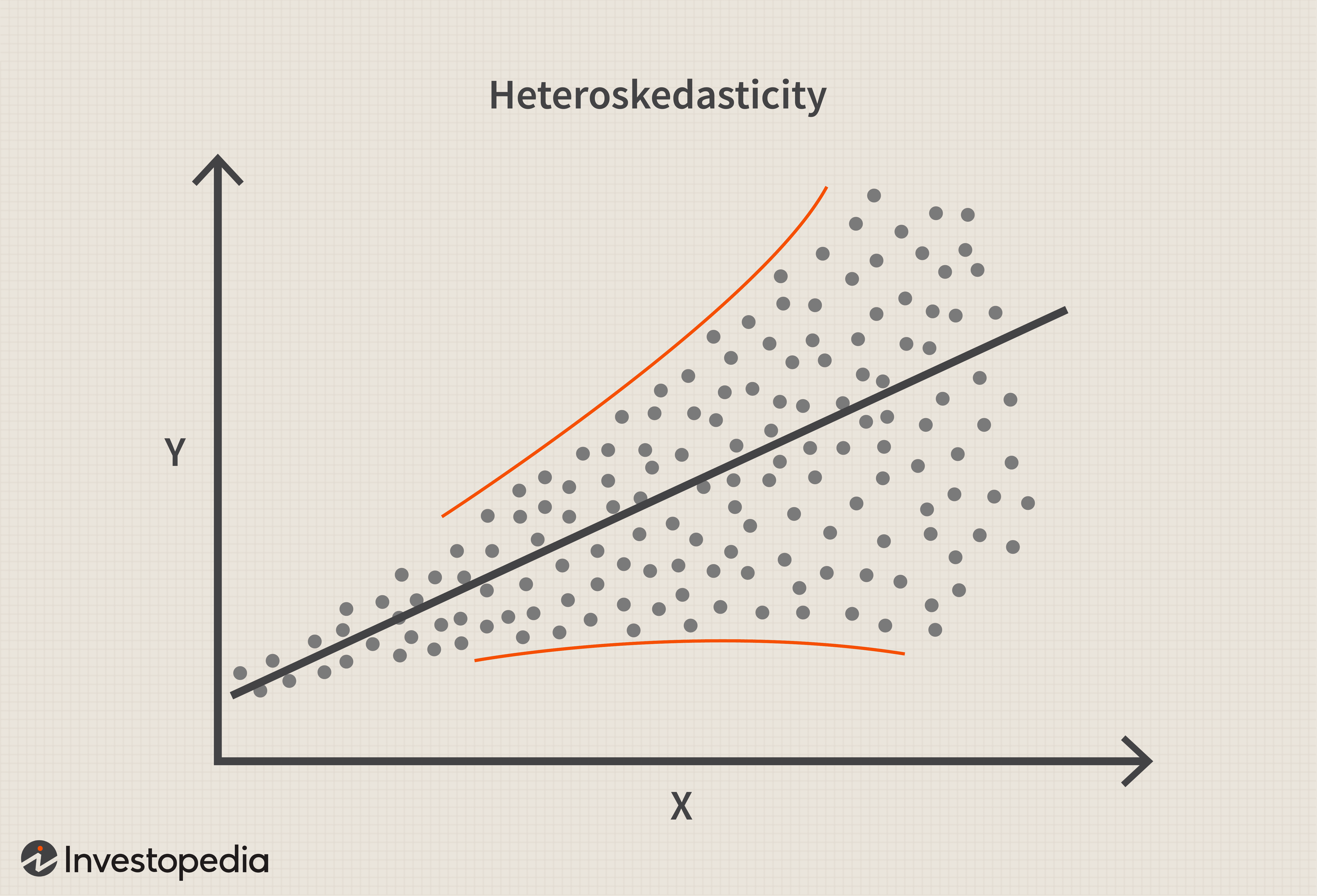
En statistiques, l'hétéroscédasticité (ou hétéroscédasticité) se produit lorsque les écarts types d'une variable prédite, surveillé sur différentes valeurs d'une variable indépendante ou en relation avec des périodes antérieures, sont non constants. Avec hétéroscédasticité, le signe révélateur lors de l'inspection visuelle des erreurs résiduelles est qu'elles auront tendance à s'estomper avec le temps, comme illustré dans l'image ci-dessous.

L'hétéroscédasticité se présente souvent sous deux formes :conditionnelle et inconditionnelle. L'hétéroscédasticité conditionnelle identifie la volatilité non constante liée à la période précédente (par exemple, quotidienne) volatilité. L'hétéroscédasticité inconditionnelle fait référence aux changements structurels généraux de la volatilité qui ne sont pas liés à la volatilité de la période précédente. L'hétéroscédasticité inconditionnelle est utilisée lorsque des périodes futures de volatilité élevée et faible peuvent être identifiées.

Points clés à retenir

• En statistiques, l'hétéroscédasticité (ou hétéroscédasticité) se produit lorsque les erreurs types d'une variable, suivi sur une durée déterminée, sont non constants.
• Avec hétéroscédasticité, le signe révélateur lors de l'inspection visuelle des erreurs résiduelles est qu'elles auront tendance à s'estomper avec le temps, comme illustré dans l'image ci-dessus.
• L'hétéroscédasticité est une violation des hypothèses de modélisation par régression linéaire, et cela peut donc avoir un impact sur la validité de l'analyse économétrique ou des modèles financiers comme le CAPM.

Bien que l'hétéroscédasticité n'entraîne pas de biais dans les estimations des coefficients, cela les rend moins précis; une précision plus faible augmente la probabilité que les estimations des coefficients soient plus éloignées de la valeur correcte de la population.

Les bases de l'hétéroscédasticité

En finance, l'hétéroscédasticité conditionnelle est souvent observée dans les prix des actions et des obligations. Le niveau de volatilité de ces actions ne peut être prédit sur aucune période. L'hétéroscédasticité inconditionnelle peut être utilisée pour discuter des variables qui ont une variabilité saisonnière identifiable, comme la consommation d'électricité.

En ce qui concerne les statistiques, hétéroscédasticité (également orthographié hétéroscédasticité) fait référence à la variance d'erreur, ou dépendance de la diffusion, dans au moins une variable indépendante au sein d'un échantillon particulier. Ces variations peuvent être utilisées pour calculer la marge d'erreur entre les ensembles de données, tels que les résultats attendus et les résultats réels, car il fournit une mesure de l'écart des points de données par rapport à la valeur moyenne.

Pour qu'un ensemble de données soit considéré comme pertinent, la majorité des points de données doivent être compris dans un certain nombre d'écarts types par rapport à la moyenne, comme décrit par le théorème de Chebyshev, également connu sous le nom d'inégalité de Chebyshev. Cela fournit des lignes directrices concernant la probabilité qu'une variable aléatoire diffère de la moyenne.

Sur la base du nombre d'écarts types spécifié, une variable aléatoire a une probabilité particulière d'exister à l'intérieur de ces points. Par exemple, il peut être nécessaire qu'une plage de deux écarts types contienne au moins 75 % des points de données pour être considérée comme valide. Une cause fréquente d'écarts en dehors de l'exigence minimale est souvent attribuée à des problèmes de qualité des données.

Le contraire d'hétéroscédastique est homoscédastique. L'homoscédasticité fait référence à une condition dans laquelle la variance du terme résiduel est constante ou presque. L'homoscédasticité est une hypothèse de la modélisation par régression linéaire. Il est nécessaire de s'assurer que les estimations sont exactes, que les limites de prédiction pour la variable dépendante sont valides, et que les intervalles de confiance et les valeurs p pour les paramètres sont valides.

Les types d'hétéroscédasticité

Inconditionnel

L'hétéroscédasticité inconditionnelle est prévisible et peut être liée à des variables de nature cyclique. Cela peut inclure des ventes au détail plus élevées signalées pendant la période de magasinage des Fêtes traditionnelle ou l'augmentation des appels de réparation de climatiseurs pendant les mois les plus chauds.

Les changements au sein de la variance peuvent être directement liés à l'occurrence d'événements particuliers ou de marqueurs prédictifs si les changements ne sont pas traditionnellement saisonniers. Cela peut être lié à une augmentation des ventes de smartphones avec la sortie d'un nouveau modèle car l'activité est cyclique en fonction de l'événement mais pas forcément déterminée par la saison.

L'hétéroscédasticité peut également concerner les cas où les données approchent d'une limite, où la variance doit nécessairement être plus petite en raison de la limite qui restreint la plage des données.

Conditionnel

L'hétéroscédasticité conditionnelle n'est pas prévisible par nature. Il n'y a aucun signe révélateur qui amène les analystes à croire que les données seront plus ou moins dispersées à tout moment. Souvent, les produits financiers sont considérés comme soumis à une hétéroscédasticité conditionnelle car tous les changements ne peuvent pas être attribués à des événements spécifiques ou à des changements saisonniers.

Une application courante de l'hétéroscédasticité conditionnelle est aux marchés boursiers, où la volatilité d'aujourd'hui est fortement liée à la volatilité d'hier. Ce modèle explique les périodes de forte volatilité persistante et de faible volatilité.

Considérations particulières

Hétéroscédasticité et modélisation financière

L'hétéroscédasticité est un concept important dans la modélisation de la régression, et dans le monde de l'investissement, des modèles de régression sont utilisés pour expliquer la performance des titres et des portefeuilles d'investissement. Le plus connu d'entre eux est le Capital Asset Pricing Model (CAPM), ce qui explique la performance d'un titre en termes de volatilité par rapport au marché dans son ensemble. Les extensions de ce modèle ont ajouté d'autres variables prédictives telles que la taille, élan, qualité, et le style (valeur versus croissance).

Ces variables prédictives ont été ajoutées car elles expliquent ou rendent compte de la variance de la variable dépendante. La performance du portefeuille est expliquée par CAPM. Par exemple, les développeurs du modèle CAPM étaient conscients que leur modèle n'expliquait pas une anomalie intéressante :des actions de haute qualité, moins volatiles que les actions de moindre qualité, avaient tendance à mieux performer que le modèle CAPM prédit. CAPM dit que les actions à haut risque devraient surperformer les actions à faible risque.

En d'autres termes, les actions à forte volatilité devraient battre les actions à faible volatilité. Mais des actions de haute qualité, qui sont moins volatiles, avaient tendance à mieux performer que prévu par CAPM.

Plus tard, d'autres chercheurs ont étendu le modèle CAPM (qui avait déjà été étendu pour inclure d'autres variables prédictives telles que la taille, style, et élan) pour inclure la qualité comme variable prédictive supplémentaire, également connu sous le nom de « facteur ». Avec ce facteur maintenant inclus dans le modèle, l'anomalie de performance des actions à faible volatilité a été prise en compte. Ces modèles, connus sous le nom de modèles multifactoriels, constituent la base de l'investissement factoriel et du bêta intelligent.